Analyze the graph of the given function f as follows:(a) Determine the end behavior: find the power function that the graph of f resembles for large values of |x|.(b) Find the x- and y-intercepts of the graph.(c) Determine whether the graph crosses or touches the x-axis at each x-intercept.(d) Graph f using a graphing utility.(e) Use the graph to determine the local maxima and local minima, if any exist. Round turning points to two decimal places.(f) Use the information obtained in (a) - (e) to draw a complete graph of f by hand. Label all intercepts and turning points.(g) Find the domain of f. Use the graph to find the range of f.(h) Use the graph to determine where f is increasing and where f is decreasing.f(x) = (x - 3)(x - 1)(x + 2)
What will be an ideal response?
(a) For large values of |x|, the graph of f(x) will resemble the graph of y = x3.
(b) y-intercept: (0, 6), x-intercepts: (-2, 0), (1, 0), and (3, 0)
(c) The graph of f crosses the x-axis at each of the intercepts (-2, 0), (1, 0), and (3, 0)
(e) Local maximum at (-0.79, 8.21); Local minimum at (2.12, -4.06)
(f) 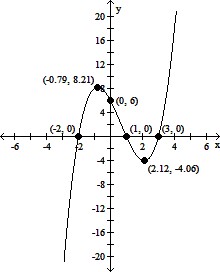
(g) Domain of f: all real numbers; range of f: all real numbers
(h) f is increasing on (-?, -0.79) and (2.12, ?); f is decreasing on (-0.79, 2.12)
You might also like to view...
Find the derivative of the function.y =  (7x + 10)3 +
(7x + 10)3 +  -1
-1
A. y ' = 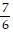 (7x + 10)2 +
(7x + 10)2 + 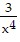
 -2
-2
B. y ' = 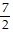 (7x + 10)2 -
(7x + 10)2 - 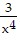
 -2
-2
C. y ' = 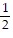 (7x)2 -
(7x)2 - 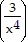 -2
-2
D. y ' =  (7x + 10)2 -
(7x + 10)2 - 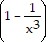 -2
-2
Find the product. Simplify the answer.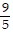 ?
? 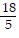
A. 
B. 
C. 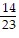
D. 
![]()
What will be an ideal response?
Solve the problem.The difference between two positive integers is 32. One integer is three times as great as the other. Find the integers.
A. 32 and 48 B. 16 and 32 C. 48 and 80 D. 16 and 48