A plane lamina with constant density (p(x,y) = 6 occupies a region in the xy-plane bounded by a simple closed path C. Its moments of inertia about the axes are  figures 4.png)
Find the moments of inertia about the axes, if C is a rectangle with vertices (0, 0), (4, 0), (4, 5) and (0, 5) .
(1000, 640)
You might also like to view...
Solve the problem.The production level P of a factory during one time period is modeled by P(x, y) = Kx1/2y1/2 where K is a positive integer, x is the number of units of labor scheduled and y is the number of units of capital invested. If labor costs $1800/unit, capital costs $600/unit and the owner has $1,800,000 available for one time period, what amount of labor and capital would maximize production?
A. 473.7 units of labor and 1285.7 units of capital B. 500.0 units of labor and 1500.0 units of capital C. 1000.0 units of labor and 3000.0 units of capital D. 1500.0 units of labor and 500.0 units of capital
Simplify the expression by using the order of operations.3 ? 9 - 2
A. 54 B. 21 C. 25 D. 29
Provide an appropriate response.Solve the proportion: 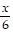 =
= 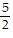
A. 0.07 B. 2.4 C. 15 D. 0.42
Evaluate the definite integral and interpret the result.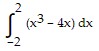
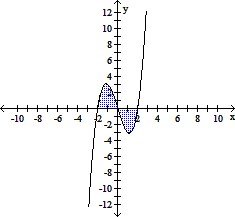
A. 4; the shaded area above the x-axis minus the shaded area below the x-axis equals 4. B. 0; the shaded area above the x-axis is equal to the shaded area below the x-axis. C. 16; the shaded area above the x-axis minus the shaded area below the x-axis equals 16. D. 16; the shaded area above the x-axis plus the shaded area below the x-axis equals 16.