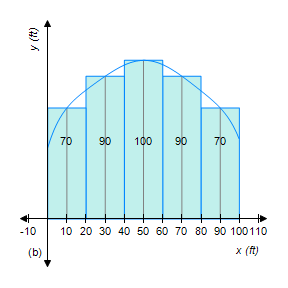
Figure (a) shows a vacant lot with a 100-ft frontage in a development. To estimate its area, we introduce a coordinate system so that the x-axis coincides with the edge of the straight road forming the lower boundary of the property, as shown in Figure (b). Then, thinking of the upper boundary of the property as the graph of a continuous function f over the interval [0, 100], we see that the problem is mathematically equivalent to that of finding the area under the graph of f on [0, 100]. To estimate the area of the lot using a Riemann sum, we divide the interval [0, 100] into five equal subintervals of length 20 ft. Then, using surveyor's equipment, we measure the distance from the midpoint of each of these subintervals to the upper boundary of the property. These measurements give the
values of f(x) at x = 10, 30, 50, 70, and 90. What is the approximate area of the lot?
?
?
?
A. 7,900 sq ft
B. 8,600 sq ft
C. 8,100 sq ft
D. 8,400 sq ft
Answer: D
Mathematics
You might also like to view...
Solve by the method of your choice. Identify whether the system has no solution or infinitely many solutions, using set notation to express the solution set.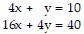
A. {(0, 10)}
B. {(5, -10)}
C. ?
D. {(x, y) 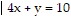 }
}
Mathematics
Determine whether the network is an Euler circuit.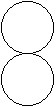
A. Yes B. No
Mathematics
Find the regression line for the given data. Round to two decimal places, if necessary.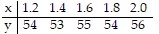
A. y = 55.3 B. y = 2.5x + 50.4 C. y = 54 D. y = 3x + 50
Mathematics
Find the perimeter.A concrete curb is to be built around a parking lot. How many meters of curbing will be needed?
A. 2500 m B. 225 m C. 125 m D. 250 m
Mathematics