Suppose that the duration of the mating calls of a population of tree toads are normally distributed, with mean 188 milliseconds (msec) and standard deviation 40 msec. What proportion of these calls would be expected to last between 192 and 268 msec? Use a table of the standard normal distribution to solve the problem. Round your answer to four decimal places.
?
A. 0.5626
B. 0.9374
C. 0.4374
D. 0.1874
E. 0.1750
Answer: C
You might also like to view...
Provide an appropriate response.Gerald made a trip to his friend's house for a birthday party. His trip is shown below, where his distance (in miles) from home is graphed as a function of the hours past 4. Refer to the graph to answer the questions about his trip.(i) When did Gerald park his car at his friend's house?(ii) How long did he stay?(iii) How far away was his friend's house?(iv) Did Gerald encounter slower traffic going to or coming home from his friend's house? 
A. (i) 5:45 (ii) One and a half hours (iii) 6 miles (iv) The traffic was heavier coming home from his friend's house since that trip took about a half an hour and the trip to his friend's house only took about 15 minutes. B. (i) 5:30 (ii) One and a half hours (iii) 12 miles (iv) The traffic was heavier going to his friend's house since that trip took about a half an hour and the trip back home only took about 15 minutes. C. (i) 5:00 (ii) One hour (iii) 12 miles (iv) The traffic was heavier going to his friend's house since that trip took about a half an hour and the trip back home only took about 15 minutes. D. (i) 6:00 (ii) Two hours (iii) 6 miles (iv) The traffic was heavier coming home from his friend's house since that trip took about a half an hour and the trip to his friend's house only took about 15 minutes.
Find the slope of a straight line that passes through the given pair of points.(-2, -14) and (19, -16)
A.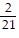 
B. -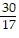 
C. -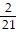 
D. -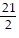 
Solve the problem.Ben Franklin bequeathed $4000.00 to the city of Boston in 1790. Assuming the fund grew to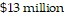 
in 200 years, find the interest rate compounded continuously that would yield this total value.
A. 2% B. 4% C. 3.1% D. 6.2%
Factor out the greatest common factor.3x(6x - 5) + 4(6x - 5)
A. (3x + 4)(6x - 5) B. (18x - 4)(x + 5) C. (18x + 4)(x - 5) D. (3x - 4)(6x + 5)