Solve the problem.A container, in the shape of an inverted right circular cone, has a radius of 6 inches at the top and a height of 9 inches. At the instant when the water in the container is 6 inches deep, the surface level is falling at the rate of -1.8 in./s. Find the rate at which water is being drained.
A. -86.4 in.3/s
B. -90.48 in.3/s
C. -98.01 in.3/s
D. -144.76 in.3/s
Answer: B
You might also like to view...
Determine whether a linear or quadratic function would be a more appropriate model for the graphed data. If linear, tell whether the slope should be positive or negative. If quadratic, decide whether the coefficient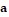 
of x2 should be positive or negative. DENTAL FLOSS USE 
Years since 1990
A. Linear; positive B. Quadratic; positive C. Linear; negative D. Quadratic; negative
Find an equation of variation for the given situation.y varies jointly as x and z and inversely as the product of w and p, and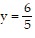 
when 
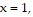
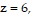
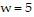and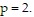 
A. y =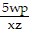 
B. y =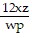 
C. y =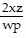 
D. y = 13pwxz
Evaluate the formula for x = -2, -1, 0, 1, and 2. Plot the resulting ordered pairs.y = -3x + 1
A. 
B.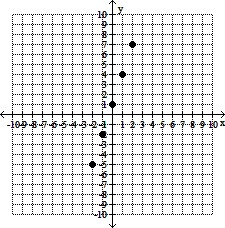 
C.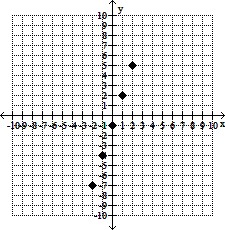 
D.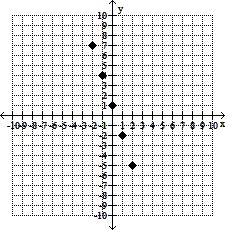 
Subtract.-12 - (-9)
A. 21 B. 3 C. -21 D. -3