Use the Principle of Mathematical Induction to show that the statement is true for all natural numbers n.5 + 5 ? 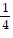 + 5 ?
+ 5 ? 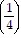 2 + ... + 5 ?
2 + ... + 5 ?  n - 1 =
n - 1 = 
What will be an ideal response?
First we show that the statement is true when n = 1.
For n = 1, we get 3 =  = 3.
= 3.
This is a true statement and Condition I is satisfied.
Next, we assume the statement holds for some k. That is,
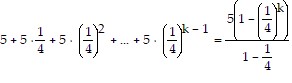 is true for some positive integer k.
is true for some positive integer k.
We need to show that the statement holds for k + 1. That is, we need to show that
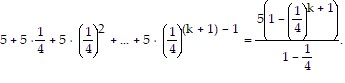
So we assume that 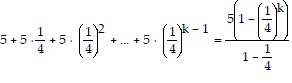 is true and add the next term,
is true and add the next term, 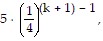 to both sides of the equation.
to both sides of the equation.
5 + 5 ? 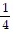 + 5 ?
+ 5 ? 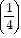 2 + ... + 5 ?
2 + ... + 5 ? 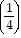 k - 1 + 5 ?
k - 1 + 5 ? 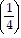 (k + 1) - 1=
(k + 1) - 1= 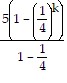 + 5 ?
+ 5 ? 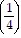 (k + 1) - 1
(k + 1) - 1
= 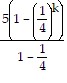 + 5
+ 5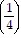 k
k
=  +
+ 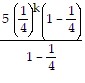
= 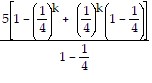
= 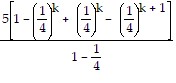
= 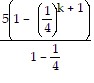
Condition II is satisfied. As a result, the statement is true for all natural numbers n.
You might also like to view...
Use your calculator to evaluate the expression. If necessary, round your answer to the nearest thousandth.e1.48
A. 15.154 B. 2.903 C. 4.393 D. 4.023
Solve the problem.An auto repair shop charged a customer $416 to repair a car. The bill listed $96 for parts and the remainder for labor. If the cost of labor is $40 per hour, how many hours of labor did it take to repair the car?
A. 7 hr B. 8 hr C. 9 hr D. 8.5 hr
Solve the problem.(a)What area does the integral 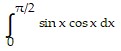 represent?(b)Use a graphing utility to approximate the area to three decimal places.
represent?(b)Use a graphing utility to approximate the area to three decimal places.
What will be an ideal response?
Solve.2x + 5 = 3(x - 1)
A. -2 B. -8 C. 2 D. 8