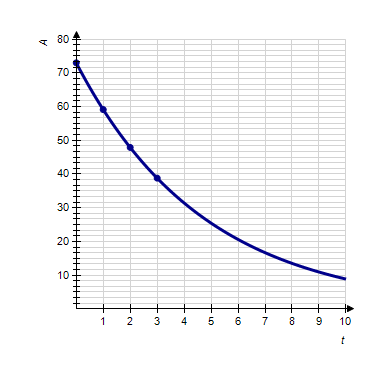
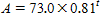The amount remaining A, in grams, of a certain radioactive is measured at monthly intervals and recorded in the table below.
t0123 A73.0059.1347.9038.80?
A: Make a table of successive ratios to show that the amount remaining of the radioactive substance can be modeled by an exponential function. Round your answer to two decimal places.B: Find an exponential model for the data. Round your answer to one decimal place.C: Plot the graph of the data points along with the exponential model. Include up to 10 months.D: According to the model, what is the half-life of this substance? That is, how long will it take for half the substance to decay? Round your answer to two decimal places.
What will be an ideal response?
?
| Time increment | From 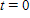 to to 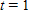 | From 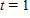 to to 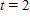 | From 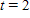 to to 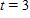 |
| Ratios of A | 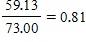 | 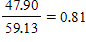 | 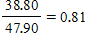 |
?
B:
C:
D: 3.29 months
You might also like to view...
Complete.46 ft =  yd
yd  ft
ft
A. 14 yd 1 ft B. 15 yd 2 ft C. 16 yd 2 ft D. 15 yd 1 ft
Find the unknown number in the proportion. Write your answer as a whole number or a mixed number if possible.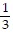 =
= 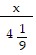
A. x = 3
B. x = 1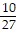
C. x = 12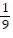
D. x = 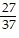
Solve the problem.Students enrolled in a prealgebra class can withdraw within the first two weeks without receiving a grade. If there were 32 students registered for class on the first day and 27 remaining at the end of the second week, what was the percent decrease in students for the first two weeks? Round to the nearest tenth of a percent, if necessary.
A. 15.6% B. 84.4% C. 18.5% D. 81.5%
Graph the rational function. Give the equations of the vertical and horizontal asymptotes.f(x) = 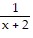
A. x = 0; y = -2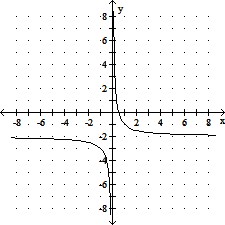
B. x = 0; y = 2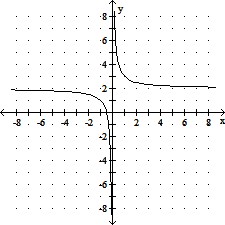
C. x = 2; y = 0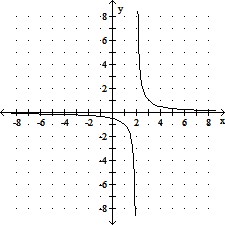
D. x = -2; y = 0