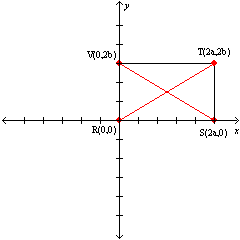
Let a and b represent positive real numbers. Use the drawing in which the vertices of rectangle RSTV are R(0,0), S(2a,0), T(2a,2b), and V(0,2b) to prove the following theorem.“The diagonals of a rectangle bisect each other.”
What will be an ideal response?
To complete the proof, we show that the midpoint of diagonal 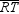 and the midpoint of diagonal
and the midpoint of diagonal 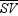 are the same point, namely the point of intersection of these diagonals.
are the same point, namely the point of intersection of these diagonals.
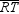 and the midpoint of diagonal
and the midpoint of diagonal 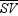 are the same point, namely the point of intersection of these diagonals.
are the same point, namely the point of intersection of these diagonals.Now 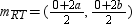
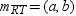
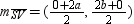
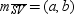
Thus, the common midpoint of 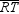
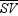
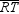
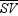
Mathematics
You might also like to view...
Fill in the blank with the correct inequality symbol. State which property of inequalities is being utilized.If x - 2 > 9, then x  11.
11.
A. x < 11; Multiplication Property B. x < 11; Addition Property C. x > 11; Addition Property D. x > 11; Multiplication Property
Mathematics
List the given numbers in order from least to greatest.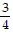 , -
, - 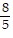 , -
, - 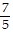 ,
, 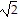 , -2
, -2
A. 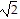 , -2,
, -2, 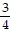 , -
, - 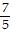 , -
, - 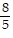
B. - 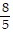 , -
, - 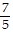 , -2,
, -2,  ,
, 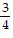
C. -2, - 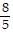 , -
, - 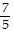 ,
, 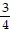 ,
, 
D. - 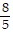 , -
, - 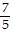 , -2,
, -2, 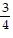 ,
, 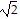
Mathematics
Use the vertex and intercepts to sketch the graph of the quadratic function.f(x) = 8 - x2 - 2x 
A. 
B. 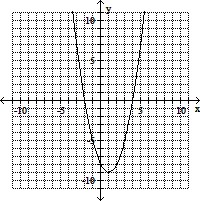
C. 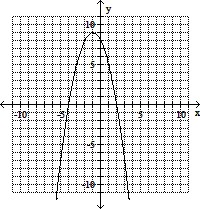
D. 
Mathematics
Find the LCM of the set of numbers.50, 80
A. 400 B. 4,000 C. 130 D. 80
Mathematics