Use the Principle of Mathematical Induction to show that the statement is true for all natural numbers n.Show that the statement "
is a prime number" is true for 
, but is not true for 
.
What will be an ideal response?
When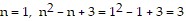 
, which is a prime number, so the statement is true when 
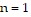. When 
, 
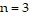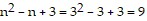, which is not a prime number, so the statement is not true for 
.
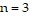You might also like to view...
Find the torsion of the space curve.r(t) = (9t sin t + 9 cos t)i + (9t cos t) - 9 sin t)j - 9k
A. ? = 1 B. ? = 0 C. Undefined D. ? = -1
Find the mode(s) for the given sample data. 99, 25, 99, 13, 25, 29, 56, 99
A. 42.5 B. 25 C. 55.6 D. 99
Use the fundamental identities and the given information to find the exact values of the remaining trigonometric functions of x.tan x = -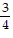 
and sec x =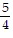 
A. sin x = -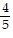 
, cos x = 
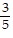, csc x = - 
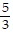, cot x = -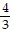 
B. sin x =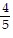 
, cos x = - 
, csc x =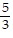 
, cot x = -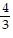 
C. sin x =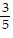 
, cos x = - 
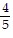, csc x = - 
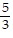, cot x =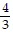 
D. sin x = -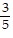 
, cos x = 
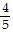, csc x = - 
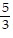, cot x = -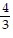 
Simplify, if possible. If the answer is undefined, state so.
A. 1 B. 2 C. -2 D. 0