Convert the polar equation to rectangular form. Identify the curve.r = 5
A. x + y = 25; a line with slope 5 and y-intercept 0
B. x2 + y2 = 25; circle centered at (0, 0) with radius 5
C. x2 - y2 = 25; circle centered at (0, 0) with radius 5
D. x + y = 5; a line with slope 5 and y-intercept 0
Answer: B
You might also like to view...
Evaluate the expression for the value of x = -4. x2 - 5x + 4 ?
A. -5 B. -40 C. 40 D. 5 E. -4
Identify the type of curve that each equation represents by evaluating B2 - 4AC. x2 - 2xy + 5y2 - 3x = 14
A. Hyperbola B. Parabola C. Ellipse
Analyze the graph of the given function f as follows:(a) Determine the end behavior: find the power function that the graph of f resembles for large values of |x|.(b) Find the x- and y-intercepts of the graph.(c) Determine whether the graph crosses or touches the x-axis at each x-intercept.(d) Graph f using a graphing utility.(e) Use the graph to determine the local maxima and local minima, if any exist. Round turning points to two decimal places.(f) Use the information obtained in (a) - (e) to draw a complete graph of f by hand. Label all intercepts and turning points.(g) Find the domain of f. Use the graph to find the range of f.(h) Use the graph to determine where f is increasing and where f is decreasing.f(x) = x2(x + 2)
What will be an ideal response?
Simplify the rational expression. Assume that no variable has a value which results in a denominator with a value of zero.
A. - 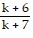
B. - 
C. 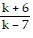
D. - 