Solve the problem.A hiker is at point A as shown in the graph and wants to take the shortest route through a field to reach a nearby road represented by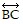 
. The shortest route will be to walk perpendicular to the road. Is 
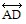the shortest route? Explain.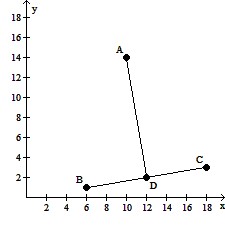
A. The product of the slopes of the two lines is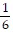 
? 
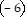, which is equal to -1, so 
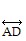is perpendicular to 
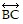and is therefore the shortest route.
B. The product of the slopes of the two lines is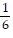 
? 
, which is equal to -1, so 
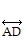is not perpendicular to 
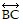and is therefore not the shortest route.
C. The product of the slopes of the two lines is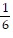 
? 6, which is equal to 1, so 
is not perpendicular to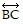 
and is therefore not the shortest route.
D. The product of the slopes of the two lines is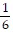 
? 6, which is equal to 1, so 
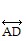is perpendicular to 
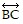and is therefore the shortest route.
Answer: A
You might also like to view...
Use the total differential dz to approximate the change in z as (x, y) moves from P to Q. Then use a calculator to find the corresponding exact change ?z (to the accuracy of your calculator).4x3y2; P(1, 1), Q(1.01, 0.99)
A. dz = 0.04; ?z = 0.0381920404 B. dz = 0.04; ?z = 0.0391920404 C. dz = 0.03; ?z = 0.0391920404 D. dz = 0.04; ?z = 0.0416920404
Factor the perfect square trinomial completely.x4 + 10x2 + 25
A. (x2 - 5)2 B. (x2 + 5)2 C. (x2 + 10)(x2 - 10) D. (x2 + 5)(x2 - 5)
Simplify by writing the expression with positive exponents. Assume that all variables represent nonzero real numbers.
A. 
B. 
C.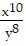 
D.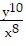 
Subtract.(16a4 - 7a2) - (10a4 + 5a2)
A. 26a4 - 2a2 B. 6a4 - 2a2 C. 6a4 - 12a2 D. -6a6