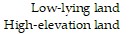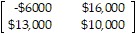Solve the problem.The table shows the population of a certain city for selected years between 1950 and 2003.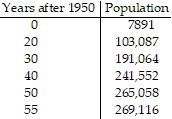 
By using your calculator to find the logistic regression equation that best fits the data, determine the limiting size of the population.
A. 271,976
B. 254,180
C. 278, 715
D. 266,078
Answer: A
You might also like to view...
Express as a sum of logarithms.log2 (4 ? 16)
A. log42 + log162 B. log2 2 + log2 4 C. log2 4 + log2 16 D. log2 4 + log2 16 + log2 2
Write the product as a sum or difference of trigonometric functions.2 sin 8x sin 17x
A. cos 9x - cos 25x
B. cos 25x + cos 9x
C.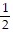 
(cos 25x + cos 9x)
D. sin 25x + sin 9x
Solve the problem.The area of a parallelogram is 12x3 + 41x2 + 39x + 7. Find a polynomial that expresses the height if the base is 4x + 7.
A. 3x2 + 5x + 7 B. 6x2 + 5x + 1 C. 3x2 + 5x + 1 D. 3x2 + 10x + 1
Prepare a payoff matrix.A farmer must decide on which of two pieces of land to grow his crops. The first piece of land has better soil and will yield a larger harvest. However this piece of land is low lying and is coastal and his crops will be destroyed in the event of a storm and flooding. The second piece of land has poorer soil but is at a higher elevation and would not be affected by flooding. If he uses the low-lying piece of land and there is no flooding he will make a profit of $16,000. If he uses the low-lying piece of land and there is flooding, he will lose $6000. If he uses the higher piece of land and there is no flooding, he will make a profit of $10,000. If he uses the higher piece of land and there is flooding, he will make a profit of $13,000. (If there is flooding
there will be a smaller supply of the crop and his profit will be higher). Prepare a payoff matrix.
A.
| Flooding | No flooding |
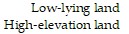
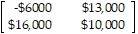
B.
| Flooding | No flooding |
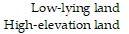
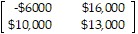
C.
| Flooding | No flooding |
