Solve the problem.An object is fired vertically upward with an initial velocity v(0) = v0 from an initial position s(0) = s0. Assuming no air resistance, the position of the object is governed by the differential equation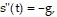 
where 
is the acceleration due to gravity (in the downward direction). For the following values of v0 and s0, find the position and velocity functions for all times at which the object is above the ground. Then find the time at which the highest point of the trajectory is reached and the height of the object at that time. v0 = 78.4 m/s, s0 =
35 m
A. s = -9.8t2 + 78.4t + 35, v = -9.8t; Highest point of 348.6 m is reached at t = 9 s
B. s = -9.8t2 + 78.4t + 35, v = -9.8t + 78.4; Highest point of 348.6 m is reached at t = 8 s
C. s = -4.9t2 + 78.4t + 35, v = -9.8t + 78.4; Highest point of 348.6 m is reached at t = 8 s
D. s = -4.9t2 + 78.4t + 35, v = -9.8t + 78.4; Highest point of 348.6 m is reached at t = 9 s
Answer: C
Mathematics
You might also like to view...
Solve the equation log 3x + log 32 = 2.
A. x = 18 B. x = 5.5 C. x = 4.5 D. x = 5 E. x = 4
Mathematics
Find the product of the complex number and its conjugate.3 - i
A. -27 B. 45 C. 3 D. 15
Mathematics
Solve the problem.Rewrite the number 0.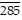
as the quotient of two integers.
A.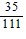 
B.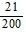 
C. 
D. 
Mathematics
Approximate the circumference of the circle using 3.14 for ?.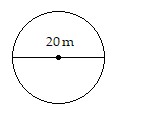
A. 62.8 m B. 125.6 m C. 64.8 m D. 129.6 m
Mathematics