Solve the problem.A drug is injected into a patient and the concentration of the drug is monitored. The drug's concentration,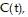 
in milligrams after t hours is modeled by 
Estimate the drug's concentration after 4 hours. (Round to the nearest hundredth.)
A. 1.71 mg
B. 0.35 mg
C. 1.58 mg
D. 0.48 mg
Answer: D
You might also like to view...
Find the general solution of the equation. Express the solution explicitly as a function of the independent variable.t-7y'(t) = 9
A. y = 72t8 + C
B. y =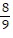 
t-8 + C
C. y = 
t8 + C
D. y = 81t9 + C
Identify the numbers from the given list that belong to the indicated set. 18, 
, -9, 0, 
, 
, 0.64, 0.
Rational numbers
A. 18, -9, 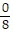0, 
, 
, 0.64, 0.
B. 18, -9, 0,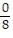 
, 
, 0.64,
C. 18, -9, 0,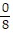 
, 0.64
D. 18, -9, 0, 
, 0.64, 0.
The energy economy of an area is composed of four industries: gas, coal, hydroelectric and nuclear. The three main consumers of energy are area residential consumers, a manufacturing plant, and a university. Assume that each consumer may use some of the energy produced by each industry, and also that each industry uses some of the energy produced by each of the other industries. The energy needs of each consumer and industry are represented by a demand vector whose entries, in order, give the amount of gas, coal, hydroelectric, and nuclear energy needed by each consumer or industry, in some convenient units. The demand vectors for the consumers are: src="https://sciemce.com/media/4/ppg__tttt0616191201__f1q183g2.jpg" alt="" style="vertical-align: -8.0px;" />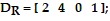 
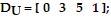and the demand vectors for the industries are: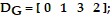 
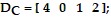
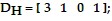
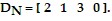Use the matrix operations on a graphing calculator to find the total demand for the four types of energy from only the consumers.
What will be an ideal response?
Solve the problem.Marty's Tee Shirt & Jacket Company is to produce a new line of jackets with an embroidery of a Great Pyrenees dog on the front. There are fixed costs of $660 to set up for production, and variable costs of $41 per jacket. Write an equation that can be used to determine the total cost, C(x), encountered by Marty's Company in producing x jackets.
A. C(x) = (660 + 41) x B. C(x) = 660 - 41x C. C(x) = 660x + 41 D. C(x) = 660 + 41x