Use mathematical induction to prove the statement is true for all positive integers n.(49)n = 49n
What will be an ideal response?
Answers may vary. Possible answer:
First we show that the statement is true when n = 1.
For n = 1, we get (49)1 = 49?1
Since 49?1 = (49)1 , P1 is true and the first condition for the principle of induction is satisfied.
Next, we assume the statement holds for some unspecified natural number k. That is,
Pk: 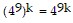 is assumed true.
is assumed true.
On the basis of the assumption that Pk is true, we need to show that Pk+1 is true.
Pk+1: (49)k+1 = 49(k+1)
So we assume that 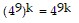 is true and multiply both sides of the equation by 49.
is true and multiply both sides of the equation by 49.
(49)k(49) = 49k(49)
(49)k+1 = 49k+9
(49)k+1 = 49(k+1).
The last equation says that Pk+1 is true if Pk is assumed to be true. Therefore, by the principle of mathematical induction, the statement (49)n = 49n is true for all natural numbers n.
You might also like to view...
Find all the first order partial derivatives for the following function.f(x, y, z) = xz
A. 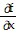 = z
= z ;
;  = -
= -  ;
; 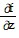 = x
= x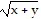
B. 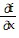 = z
= z ;
; 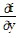 = -
= -  ;
; 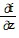 = x
= x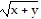
C. 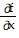 = z
= z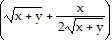 ;
; 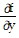 =
=  ;
;  = x
= x
D.  = z
= z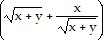 ;
;  =
=  ;
;  = x
= x
Divide. Write the answer in lowest terms.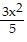 ÷
÷ 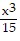
A. 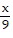
B. 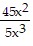
C. 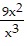
D. 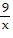
If the infinite curve 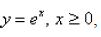 is rotated about the x-axis , find the area of the resulting surface. Select the correct answer.
is rotated about the x-axis , find the area of the resulting surface. Select the correct answer.
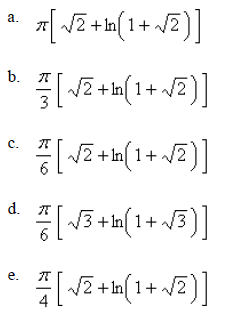
Solve the problem.The velocity of particle A, t seconds after its release is given by 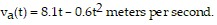 The velocity of particle B, t seconds after its release is given by
The velocity of particle B, t seconds after its release is given by 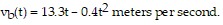 If velocity is measured in meters per second, how much farther does particle B travel than particle A during the first ten seconds (from
If velocity is measured in meters per second, how much farther does particle B travel than particle A during the first ten seconds (from 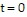 to
to 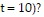 Round to the nearest meter.
Round to the nearest meter.
A. 720 m B. 4 m C. 327 m D. 460 m