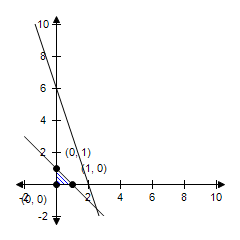
The linear programming problem has an unusual characteristic. Select a graph of the solution region for the problem and describe the unusual characteristic. Find the maximum value of the objective function (if possible) and where it occurs.
?
z = 3x + 4y
?
Constraints:
?
x ? 0
y ? 0
x + y ?1
3x + y ? 6
?
A. ?
The constraint 3x + y ? 6 is extraneous. Maximum at (1, 1): 7
B. ?
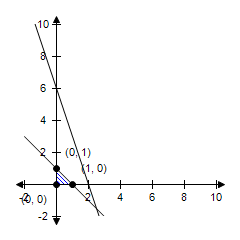
The constraint 3x + y ? 6 is extraneous. Maximum at (1, 0): 3
C. ?
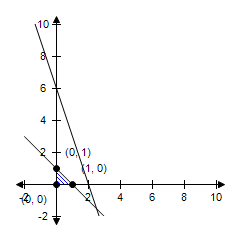
The constraint 3x + y ? 6 is extraneous. Maximum at (0, 1): 4
D. ?
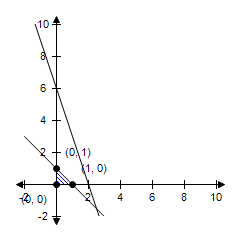
The constraint 3x + y ? 6 is extraneous. Maximum at (0, 0): 0
E. ?
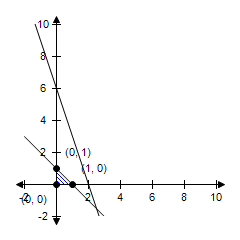
The constraint 3x + y ? 6 is extraneous. No maximum.
Answer: C
You might also like to view...
Evaluate the integral by using a substitution prior to integration by parts.
A. x[cos (ln x) + sin (ln x)] + C
B.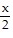 
[cos (ln x) - sin (ln x)] + C
C. x cos (ln x) + sin (ln x)+ C
D. 
[cos (ln x) + sin (ln x)] + C
Write using exponential notation.6 ? 6
A. 62 B. 26 C. 63 D. 2 ? 6
Solve the problem.In one country, it is estimated that in the year 2050, 9% of the population will be over 70. If the population of this country in 2050 is 446 million, how many people will be over 70?
A. 35.68 million B. 401.40 million C. 40.14 million D. 44.60 million
Use the commutative property of multiplication to write an equivalent algebraic expression.3x + 6
A. 3 + 6x B. 6 + 3x C. x3 + 6 D. 6 + x3