Suppose Ingredient I is made up of 80% micoden and 20% water, Ingredient II is made up of 30% micoden, 50% bixon, and 20% water, and these ingredients are mixed together. How much micoden is in the mixture?
INGREDIENT I INGREDIENT II MIXTURE 2 lb 11 lb 13 lb?
A. 1.6 lb
B. 4.9 lb
C. 2.2 lb
D. 13 lb
E. 3.3 lb
Answer: B
You might also like to view...
Find dy/dx by implicit differentiation. If applicable, express the result in terms of x and y.x2y5 + 9y = 9x - 1
A. 
B. 
C. 
D. 
Solve the problem.A furniture company makes two different types of lamp stands. Each lamp stand A requires 11 minutes for sanding, 18 minutes for assembly, and 8 minutes for packaging. Each lamp stand B requires 13 minutes for sanding, 23 minutes for assembly, and 7 minutes for packaging. The total number of minutes available each day in each department are as follows: for sanding 4000 minutes, for assembly 8000 minutes, and for packaging 2000 minutes. The profit on each lamp stand A is $19 and the profit on each lamp stand B is $27. How many of each type of lamp stand should the company make per day to maximize their profit? Set this up as a linear programming problem in the following form: Maximize cTx subject to Ax ? b and x ? 0. Do not find the solution.
A. Let x1 be the number of lamp stands of type A made per day and x2 the number of lamp stands of type B made per day.
Then b = , x =
, x = 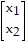 , c =
, c =  , and A =
, and A = 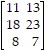
B. Let x1 be the number of lamp stands of type A made per day and x2 the number of lamp stands of type B made per day.
Then b = 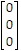 , x =
, x = 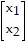 , c =
, c =  , and A =
, and A = 
C. Let x1 be the number of lamp stands of type A made per day and x2 the number of lamp stands of type B made per day.
Then b =  , x =
, x = 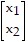 , c =
, c =  , and A =
, and A = 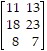
D. Let x1 be the number of lamp stands of type A made per day and x2 the number of lamp stands of type B made per day.
Then b =  , x =
, x = 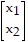 , c =
, c =  , and A =
, and A = 
Write the number in scientific notation.33,000
A. 3.3 × 103 B. 3.3 × 10-4 C. 3.3 × 104 D. 3.3 × 10-3
Translate to an algebraic expression.Alan weighs 3 times as much as his son. Let x represent Alan's weight. Write an expression for the weight of Alan's son.
A. 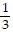 x
x
B. 3x
C. 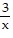
D. x - 3