Solve the problem.A company manufactures two ballpoint pens, silver and gold. The silver requires 4 min in a grinder and 6 min in a bonder. The gold requires 5 min in a grinder and 7 min in a bonder. The grinder can be run no more than 53 hours per week and the bonder no more than 54 hours per week. The company makes a $3 profit on each silver pen sold and $12 on each gold. How many of each type should be made each week to maximize profits?
A. Silver pens: 462
Gold pens: 218
B. Silver pens: 1
Gold pens: 462
C. Silver pens: 0
Gold pens: 461
D. Silver pens: 218
Gold pens: 461
Answer: B
You might also like to view...
Use reduction formulas to evaluate the integral.
A.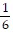 
sec 3x tan 3x + 
ln
+ C
B. 
sec2 3x tan 3x + 
ln
+ C
C. 
sec 3x tan 3x + 
ln
+ C
D. 
sec 3x tan 3x - 
ln
+ C
Solve the linear inequality. Express the solution in set-builder notation.-7x - 3 > -8x + 6
A. {x|x < 9} B. {x|x > 3} C. {x|x > 9} D. {x|x < 3}
Find an equation for the line, in the indicated form, with the given properties. Containing the points (-5, 0) and (5, 3); general form
A. 5x - 2y = 31 B. -3x - 10y = -15 C. -5x + 2y = 31 D. 3x - 10y = -15
Find the expected value.Suppose that 1,000 tickets are sold for a raffle that has the following prizes: one $300 prize, two $100 prizes, and one hundred $1 prizes. What is expected value of a ticket?
A. $300 B. $0.60 C. $1 D. $100