Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator.logb (yz5)
A. logb y + 5 logb z
B. 5 logb yz
C. 5 logb y + 5 logb z
D. logb y + logb5z
Answer: A
You might also like to view...
Find the average value of the function over the given interval.f(x) = 10x on [9, 11]
A. 100 B. 50 C. 400 D. 200
Solve the problem.The width of a rectangular computer screen is 2 inches more than its height. If the area of the screen is 195 square inches, find its dimensions.
A. 13 in. by 15 in. B. 14 in. by 14 in. C. 12 in. by 16 in. D. 26 in. by 7.5 in.
Provide an appropriate response.The process of amortization includes which of the following?
A. a specific length of time B. equal payments C. variable rates D. both equal payments and a specific length of time
Solve the problem.A space heater can raise the temperature in a room by 2°F every 5 minutes. The temperature in the room was 69°F after the heater had been running for 10 minutes. (i) Write as a linear equation in slope-intercept form the relationship between the time that the heater has been running and the temperature in the room.(ii) Explain how you could have predicted whether the slope of the graph of this equation is positive or negative.
A. (i) y =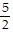 
x - 65
(ii) As the amount of time the space heater is left on increases, the temperature of the room increases, which implies a positive slope.
B. (i) y =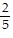 
x + 65
(ii) As the amount of time the space heater is left on increases, the temperature of the room increases, which implies a positive slope.
C. (i) y =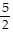 
x + 65
(ii) As the amount of time the space heater is left on increases, the temperature of the room increases, which implies a positive slope.
D. (i) y =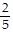 
x - 65
(ii) As the amount of time the space heater is left on increases, the temperature of the room increases, which implies a positive slope.