Solve the problem.Cory and Melissa are racing electronic cars around a circular track. They begin at the same time going in the same direction. Cory's car completes a revolution in 40 seconds, while Melissa's car completes a revolution in 35 seconds. How long will it take them before both cars reach the starting point again simultaneously?
A. 560 sec
B. 280 sec
C. 112 sec
D. 56 sec
Answer: B
You might also like to view...
Find the directional derivative of the function f(x,y) =  figures 4.png)
at the point p(7, 0) in the direction of the unit vector that makes the angle  figure.png)
with the positive x-axis.
 multiple choice.png)
Evaluate the integral by changing the order of integration in an appropriate way.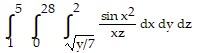
A.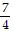 
ln 5 (1 - sin 4)
B.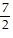 
ln 5 (1 - cos 4)
C.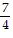 
ln 5 (1 - cos 4)
D.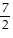 
ln 5 (1 - sin 4)
Evaluate. Assume that all variables represent positive numbers. |-8.5|
A. -8.5 B. 17 C. 8.5 D. 0
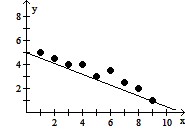
Solve the problem.For the following table of data, a.Draw a scatterplot.b.Calculate the correlation coefficient.c.Calculate the least squares line and graph it on the scatterplot.d.Predict the y-value when x is 15.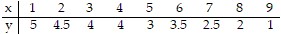
?
A. a.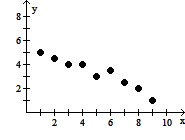
b. 0.965
c. Y = 0.45x - 5.53
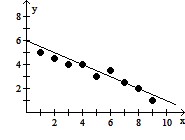
d. 1.22
B. a.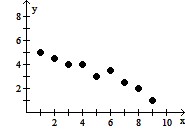
b. -0.965
c. Y = -0.45x - 5.53
d. -12.28
C. a.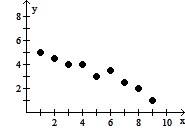
b. 0.965
c. Y = -0.45x + 5.53
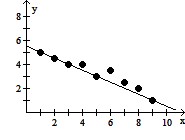
d. -1.22
D. a.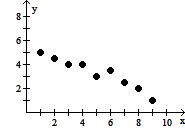
b. -0.965
c. Y = -0.45x + 5.53
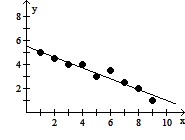
d. -1.22