Solve the problem.Rachel's bus leaves at 2:20 PM and accelerates at the rate of 3 meters per second per second. Rachel, who can run 7 meters per second, arrives at the bus station 3 seconds after the bus has left. Find parametric equations that describe the motions of the bus and Rachel as a function of time. Determine algebraically whether Rachel will catch the bus. If so, when?
A. Bus: x1 =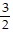 
t2, y1 = 1; Rachel: x2 = 7(t - 3), y2 = 3
Rachel won't catch the bus.
B. Bus: x1 = 3t2, y1 = 1; Rachel: x2 =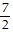 
(t - 3), y2 = 3
Rachel will catch the bus at 2:24 PM
C. Bus: x1 = 
t2, y1 = 1; Rachel: x2 = 7(t + 3), y2 = 3
Rachel won't catch the bus.
D. Bus: x1 = t2, y1 = 1; Rachel: x2 = 7(t - 3), y2 = 3
Rachel will catch the bus at 2:25 PM
Answer: A
You might also like to view...
Find the first term and the common difference of the arithmetic sequence described. Give a formula for the nth term of the sequence.4th term is 8; 6th term is 18
A. a = -2; d = 5; an = 5n - 7 B. a = 7; d = -5; an = 5n + 12 C. a = -7; d = 5; an = 5n - 12 D. a = -2; d = 5; an = -7n + 5
The graph of a one-to-one function is given. Draw the graph of the inverse function f-1. For convenience, the graph of 
is also give.
A. 
B.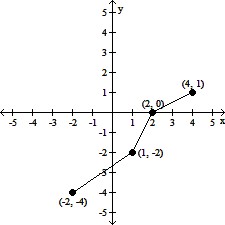 
C.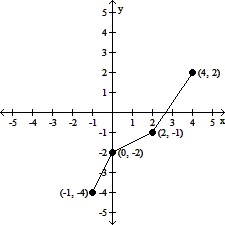 
D. 
Match the given graph with its equation.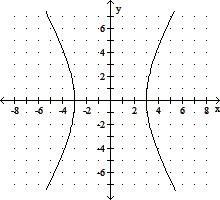
A.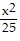 
- 
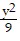= 1
B. 
- 
= 1
C. 
+ 
= 1
D. 
- 
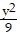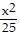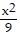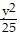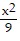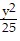= 1
Solve.A railroad tunnel is shaped like a semi-ellipse. The height of the tunnel at the center is 60 ft and the vertical clearance must be 30 ft at a point 9 ft from the center. Find an equation for the ellipse.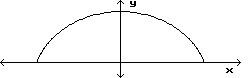
A.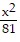 
+ 
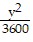= 1
B. 
+ 
= 1
C. 
+ 
= 1
D. 
+ 
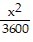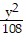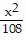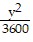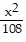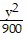= 1