Solve the linear programming problem.The Fiedler family has up to $130,000 to invest. They decide that they want to have at least $40,000 invested in stable bonds yielding 5.5% and that no more than $60,000 should be invested in more volatile bonds yielding 11%. How much should they invest in each type of bond to maximize income if the amount in the stable bond should not exceed the amount in the more volatile bond? What is the maximum income?
What will be an ideal response?
$60,000 in the stable bonds and $60,000 in the volatile bonds; maximum income $9900
You might also like to view...
Solve.Newton's Law of Cooling states that if a body with temperature T1 is placed in surroundings with temperature T0 different from T1, then the body will either cool or warm to temperature T(t) after time t, in minutes, where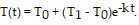 
A cup of coffee with temperature 105°F is placed in a freezer with temperature 0°F. After 5 minutes, the temperature of the coffee is 69.3°F. What will its temperature be 20 minutes after it is placed in the freezer? Round your answer to the nearest degree.
A. 20°F B. 16°F C. 17°F D. 18°F
Solve the equation for the specified variable.A = P(1 + nr) for r
A. r = 
B. r = 
C. r =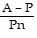 
D. r = 
Consider the function h as defined. Find functions f and g such that (f ? g)(x) = h(x).h(x) =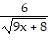 
A. f(x) =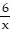 
, g(x) = 9x + 8
B. f(x) =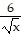 
, g(x) = 9x + 8
C. f(x) = 6, g(x) =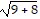 
D. f(x) =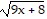 
, g(x) = 6
Write the polynomial in standard form and determine its degree.-4x2 - 8x3 - 20x4 + 9 + x
A. 12 + x - 4x2 - 8x3 - 20x4, degree 4 B. x + -4x2 - 8x3 - 20x4 + 9, degree 9 C. -20x4 - 8x3 - 4x2 + x + 9, degree 4 D. -20x4 - 8x3 - 4x2 + x + 9, degree 10