Find, if possible, the (global) maximum and minimum values of the given function on the indicated interval.f(x) = x - 2 on [-3, 4]
A. Maximum value f(4) = 2; minimum value f(-3) = - 5
B. Maximum value f(-3) = 2; minimum value f(4) = - 1
C. Maximum value f(4) = 6; minimum value f(-3) = - 1
D. Maximum value f(-4) = 6; minimum value f(3) = - 5
Answer: A
You might also like to view...
Solve the problem.Two bicyclists, 42 miles apart, begin riding toward each other on a long straight avenue. One cyclist travels 15 miles per hour and the other 20 miles per hour. At the same time, Spot (a greyhound), starting at one cyclist, runs back and forth between the two cyclists as they approach each other. If Spot runs 38 miles per hour and turns around instantly at each cyclist, how far has he run when the cyclists meet?
Fill in the blank(s) with the appropriate word(s).
Factor.x2 - x - 48
A. (x + 6)(x - 8) B. (x - 6)(x + 8) C. (x - 48)(x + 1) D. Not factorable
Find projwv.v = 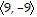 , w =
, w = 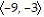
A. 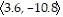
B. 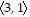
C. 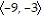
D. 
Find the center and radius of the circle.2x2 + 2y2 - 8x - 16y + 22 = 0
A. (-2, -4), r = 9 B. (4, 2), r = 3 C. (-4, -2), r = 9 D. (2, 4), r = 3