The result of a hypothesis is described in terms of the probability of obtaining a particular sample. Use the given context to formulate the null and alternative hypotheses. Discuss whether the sample provides evidence for rejecting the null hypothesis.A consumer group believes that the mean volume of juice in a company's 24 ounce juice bottles is actually less than 24 ounces.In a random sample of 310 bottles, the mean volume of juice was 23.9 ounces. Assuming that the mean volume of juice for all the company's 24-ounce bottles is 24 ounces, the probability of selecting a random sample with a mean volume of 23.9 ounces or less is 0.00017.
What will be an ideal response?
Null hypothesis: mean volume of juice in 24-ounce bottles is 24 ounces
Alternative hypothesis: mean volume of juice in 24-ounce bottles is less than 24 ounces
The results is significant at the 0.01 level. There is strong evidence for rejecting the null hypothesis in favor of the alternative hypothesis that the mean volume is less than 24 ounces.
You might also like to view...
Solve the problem.Refer to the following preference schedule.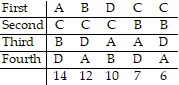
Find the winner of a sequential runoff.
A. D B. A C. B D. C
Solve the system. If there is an unlimited number of solutions, find one of them.x + y + z = 1x - y + 2z = -14x + 4y + 4z = 13
A. x = 4, y = 1, z = -4 B. x = -4, y = 4, z = 1 C. x = -4, y = 1, z = 4 D. Inconsistent
Find the inverse of the function.f(x) =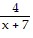 
A. f-1(x) =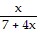 
B. Not a one-to-one function
C. f-1(x) =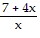 
D. f-1(x) =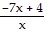 
Determine whether the following is always true or not always true. Given reasons for your answers.(u × v) ? w = u ? (w × v)
What will be an ideal response?