Solve the problem.With the function f(x) = logax, why can't x be less than 0?
What will be an ideal response?
Answers may vary. One possibility: The function is defined for all positive numbers a,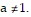 
Since a positive number raised to any real-number exponent is a positive number, x must be positive, too. That begs the question of why a must be positive. Assume that a is a negative number. A negative number raised to certain powers (e.g., 1/2) would yield a non-real number.
You might also like to view...
Graph the inverse function.y = sec-1 2x
A.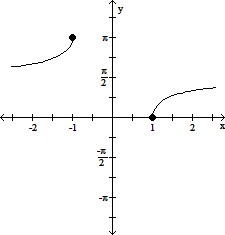 
B.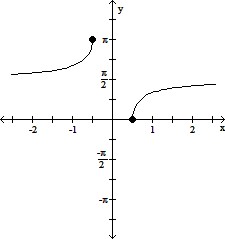 
C.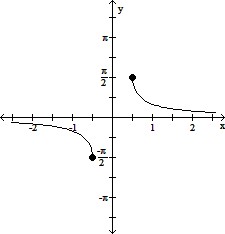 
D.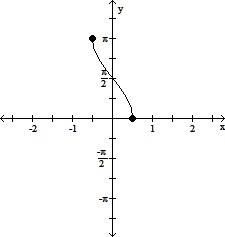 
Solve the problem algebraically. Clearly define all variables, write an appropriate equaion, and solve.A triangular-shaped stained glass window has two sides that are each 36 inches shorter than four times the length of the shortest side. If the perimeter of the window is 198 inches, what are the lengths of the three sides?
A. 30 inches, 84 inches, 84 inches B. 30 inches, 120 inches, 120 inches C. 30 inches, 54 inches, 54 inches D. 30 inches, 96 inches, 96 inches
Which of the following IS NOT an example of an exit barrier?
A. switching costs B. fixed costs of exit, such as labor agreements C. emotional barriers D. specialized assets
Suppose that the function with the given graph is not f(x), but f'(x). Find the open intervals where the function is concave upward or concave downward, and find the location of any inflection points.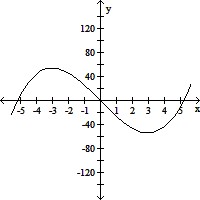
A. Concave upward on (-?, -3) and (3, ?); concave downward on (-3, 3); inflection points at -20 and 20 B. Concave upward on (-?, 0); concave downward on (0, ?); inflection point at 0 C. Concave upward on (-3, 3); concave downward on (-?, -3) and (3, ?); inflection points at -3 and 3 D. Concave upward on (-?, -3) and (3, ?); concave downward on (-3, 3); inflection points at -3 and 3