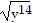Solve the problem.Assuming all the necessary derivatives exist, show that if 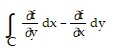 = 0 closed curves C to which Green's Theorem applies, then f satisfies the Laplace equation
= 0 closed curves C to which Green's Theorem applies, then f satisfies the Laplace equation  +
+  = 0 for all regions bounded by closed curves C to which Green's Theorem applies.
= 0 for all regions bounded by closed curves C to which Green's Theorem applies.
What will be an ideal response?
Let C be a closed curve for which Green's Theorem applies. Then 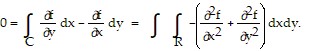 If the Laplace equation does not hold for f on R, then there is a simple closed curve C' in the interior of R which bounds a simply connected region R' on which
If the Laplace equation does not hold for f on R, then there is a simple closed curve C' in the interior of R which bounds a simply connected region R' on which 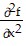 +
+ 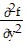 ? 0 for all (x, y) in R'. Moreover, without loss of generality, we can assume that
? 0 for all (x, y) in R'. Moreover, without loss of generality, we can assume that 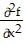 +
+ 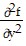 > 0 . Hence
> 0 . Hence 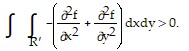 As Green's Theorem applies to C', we also have that
As Green's Theorem applies to C', we also have that
0 =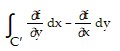 =
=  which is a contradiction.
which is a contradiction.
You might also like to view...
Answer the question.Use the equation 5x2 + 2x = c to explain how to solve a quadratic equation by completing the square.
What will be an ideal response?
Provide an appropriate response.Solve the system of equations by graphing:2x - y = 5-4x + 2y = 8
A.

B. 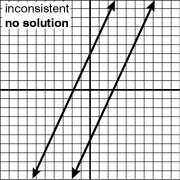
C. 
D. 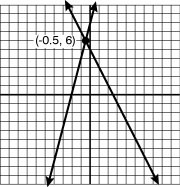
Perform the operation and reduce to lowest terms.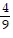 ×
× 
A. 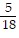
B. 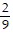
C. 
D. 
Write using radical notation. Then, simplify, if possible.(25y14)1/2
A. 5y14
B. 5y7
C. 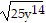
D. 5