A certain animal grows to a maximum length of 28 inches. Its length, in inches, at age 
years is given by the function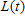 
. The difference
src="https://sciemce.com/media/3/ppg__cognero__Section_6.4_Equations_of_Change_Linear_and_Exponential_Functions__media__880d031b-fe53-4676-9f4b-a6ab67b6d679.PNG" class="wirisformula" align="middle" style="vertical-align: middle;" data-wiris-created="true" varid="variable_id_field" variablename="impvar_a1f2bc38aca54c8a9e58b15b3" /> between the maximum length and the current length satisfies the equation of change
.
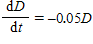A: If the animal is 5 inches long when it is born, find a formula that gives the length difference D as a function of the age t. Write your answer using the alternative form for an exponential function.B: Find a formula that gives the length in terms of the age.C: What is the animal's length at age 8 years?
What will be an ideal response?
?A: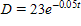 
?
B: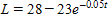 
?
C: 12.58 inches
Mathematics
src="https://sciemce.com/media/3/ppg__cognero__Section_6.4_Equations_of_Change_Linear_and_Exponential_Functions__media__880d031b-fe53-4676-9f4b-a6ab67b6d679.PNG" class="wirisformula" align="middle" style="vertical-align: middle;" data-wiris-created="true" varid="variable_id_field" variablename="impvar_a1f2bc38aca54c8a9e58b15b3" /> between the maximum length and the current length satisfies the equation of change
.
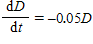
A: If the animal is 5 inches long when it is born, find a formula that gives the length difference D as a function of the age t. Write your answer using the alternative form for an exponential function.B: Find a formula that gives the length in terms of the age.C: What is the animal's length at age 8 years?
What will be an ideal response?
A:
?
B:
?
C: 12.58 inches
You might also like to view...
Find an approximate equation y = abx of the exponential curve that contains the given pair of points. Round the values of a and/or b to two decimal places, if necessary.(0, 5.2) and (3, 87.2)
A. y = 5.2(3.07)x B. y = 5.2(50.31)x C. y = 5.2(2.56)x D. y = 5.2(5.59)x
Factor.8z2 - 6z - 9
A. (4z + 3)(2z - 3) B. Prime C. (8z + 3)(z - 3) D. (4z - 3)(2z + 3)
Provide an appropriate response.The demand function for a manufacturer's product is given by p = 500 - 5q - q2 where p is the price per unit when q units are demanded. The point elasticity of demand when q = 5 is
A. -1.5. B. -0.5. C. -6. D. -1. E. -4.
Solve the problem.Atomic nuclei consist of protons and neutrons. The number of protons and neutrons in a particular nucleus must fall into a well-defined range of values in order for the nucleus to be stable, else it will be unstable and will disintegrate by radioactive decay. The figure below shows this so-called "region of stability" for nuclei having proton numbers between 10 and 60. Using the figure, comment on the stability of a nucleus that contains 35 protons and 50 neutrons.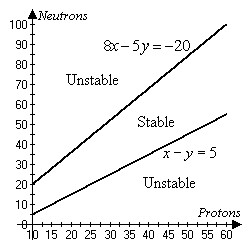
A. The nucleus falls within the region of stability and therefore will be radioactive. B. The nucleus falls outside the region of stability and therefore will be radioactive. C. The nucleus falls outside the region of stability and therefore will be nonradioactive. D. The nucleus falls within the region of stability and therefore will be nonradioactive.