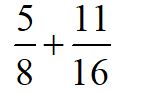cos 52°
A. 0.71
B. -0.16
C. -0.07
D. 0.62
Answer: D
You might also like to view...
Solve the problem.The differential equation for a falling body near the earth's surface with air resistance proportional to the velocity v is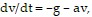 
where g = 32 feet per second per second is the acceleration due to gravity and a > 0 is the drag coefficient. This equation can be solved to obtain v(t) = (v0 - v?)e-at + v?, where v0 = v(0) and v? = -g/a = 
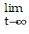v(t), the terminal velocity.This equation, in turn, can be solved to obtain y(t) = y0 + tv? + (1/a)(v0 - v?)(1 - e-at) where y(t) denotes the altitude at time t. Suppose that a ball is thrown straight
up from ground level with an initial velocity v0 and drag coefficient a. Find an expression in terms of v0, g, and a for the time at which the ball reaches its maximum height.
A. t =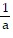 
ln 
B. t = 
ln 
C. t = 
ln 
D. t = 
ln 
Write the percent as a fraction in the lowest terms.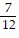
%
A. 
B. 
C.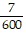 
D.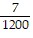 
Graph the inequality.2x + 4y ? -8
A.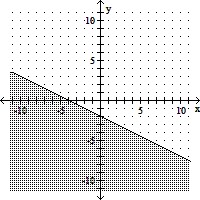 
B.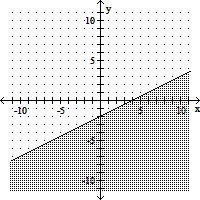 
C.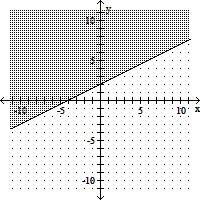 
D.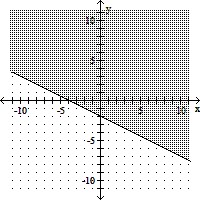 
Add:
