One or more zeros of the polynomial are given. Find all remaining zeros.P(x) = x3 + 2x2 - 11x - 52; 4 is a zero
A. -3 + 2i, -3 - 2i
B. 2 + i, 2 - i
C. -3 +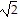 
, -3 -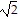 
D. -3 + i, -3 - i
Answer: A
You might also like to view...
Solve the equations by factoring.8k2 - 15k - 2 = 0
A. -8, 2
B. -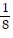 
, 2
C. - 
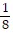, 8
D.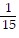 
, - 
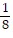
For the given equation, do the following:(a) Simplify the expression on each side of the equal sign. (b) See if 5 is a solution to both the given equation and the equation formed in part (a).x2 + 3x2 = 12x + 8x
A. (a) 4x2 = 25x; (b) 5 only checks in the given equation. B. (a) 4x2 = 20x; (b) 5 does not check in either equation. C. (a) 3x2 = 20x; (b) 5 only checks in the given equation. D. (a) 4x2 = 20x; (b) 5 checks in both equations.
Find the circle's circumference or area, as requested. Use 3.14 as the approximate value of ?, and round your answer to the nearest tenth.Find the circumference.
A. 53.4 mi B. 106.8 mi C. 26.7 mi D. 226.9 mi
Use a graphing utility to graph the function over the indicated interval and approximate any local maxima and local minima. If necessary, round answers to two decimal places.f(x) = x4 - 5x3 + 3x2 + 9x - 3; (-5, 5)
A. local minimum at (-3, -3) local maximum at (-1.32, 5.64) local minimum at (0.57, -6.12) B. local minimum at (-0.61, -5.64) local maximum at (1.41, 6.12) local minimum at (3, -3) C. local minimum at (-0.57, -6.12) local maximum at (1.32, 5.64) local minimum at (3, -3) D. local minimum at (-1, -6) local maximum at (1, 6) local minimum at (3, -3)