Find |v| and |u + v|, given that u = -j and v = i.
 figure 1.png)
 answer.png)
You might also like to view...
Solve the given trigonometric equation analytically (using identities when necessary for exact values when possible) for values of x for 0 ? x < 2?.sec2 x - 2 = tan2 x
A. 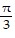
B. 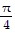
C. No solution
D. 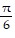
Solve the problem.Mary lives on a corner lot. The neighborhood children have been cutting diagonally across her lawn instead of walking around the yard. If the diagonal distance across the lawn is and the longer part of the sidewalk is twice the shorter length, how many feet are the children saving by cutting across the lawn? Round to the nearest foot if necessary.
A. 40 ft B. 13 ft C. 17 ft D. 10 ft
An objective function and a system of linear inequalities representing constraints are given. Graph the system of inequalities representing the constraints. Find the value of the objective function at each corner of the graphed region. Use these values to determine the maximum value of the objective function and the values of x and y for which the maximum occurs.Objective Functionz = 15x + 12yConstraints0 ? x ? 10 0 ? y ? 5 3x + 2y ? 6
A. maximum: 60; at (0, 5) B. maximum: 36; at (0, 3) C. maximum: 150; at (10, 0) D. maximum: 210; at (10, 5)
Transform the polar equation to an equation in rectangular coordinates. Then identify and graph the equation.r sec ? = -6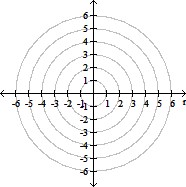
A. 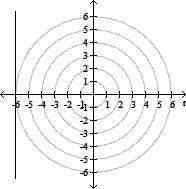
x = -6; vertical line 6 units
to the left of the pole
B. 
(x + 3)2 + y2 = 9; circle, radius 3
center (-3, 0) in rectangular coordinates
C. 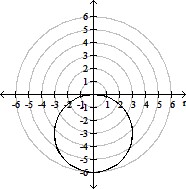
x2 + (y + 3)2 = 9; circle, radius 3,
center at (0, -3) in rectangular coordinates
D. 
y = -6; horizontal line 6 units
below the pole