Solve the problem.For what numbers x, 0 ? x ? 2?, does cos x = -1?
A. ?
B.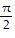 
C.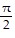 
, 
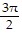
D. none
Answer: A
You might also like to view...
Provide an appropriate response.Use the fact that the hypotenuse is the longest side of a right triangle to explain why the sine or cosine of an angle will never be greater than one.
What will be an ideal response?
Use the table to determine the probability. Round your answer to three decimal places if necessary.The table gives the number of degrees earned in a certain university in the 2007-2008 academic year.
If a student receiving a degree is randomly selected, what is the probability the degree recipient selected is a female or earned a Doctorate?
A. 0.016 B. 0.597 C. 0.588 D. 0.009
Set the viewing rectangle of your graphing calculator to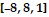 
by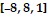 
to solve the problem.Find a set of parametric equations evaluated over 0 ? t ? 2? that produces the graph shown.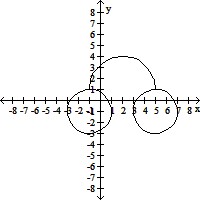
A.
| x1 = -1 + 2cos(t), | y1 = -1 + 2sin(t) |
| x2 = 3 + 2cos(t), | y2 = -1 + 2sin(t) |
| x3 = 1 + 3cos(0.5t), | y3 = 1 + 3sin(0.5t) |
B.
| x1 = -1 + 2cos(t), | y1 = -1 + 2sin(t) |
| x2 = 5 + 2cos(t), | y2 = -1 + 2sin(t) |
| x3 = 2 + 3cos(t), | y3 = 1 + 3sin(t) |
C.
| x1 = -1 + 2cos(t), | y1 = -1 + 2sin(t) |
| x2 = 5 + 2cos(t), | y2 = -1 + 2sin(t) |
| x3 = 2 + 2cos(0.5t), | y3 = 1 + 2sin(0.5t) |
D.
| x1 = -1 + 2cos(t), | y1 = -1 + 2sin(t) |
| x2 = 5 + 2cos(t), | y2 = -1 + 2sin(t) |
| x3 = 2 + 3cos(0.5t), | y3 = 1 + 3sin(0.5t) |
Solve the system by graphing. 3x - 2y = 4-6x + 4y = 7
A. x = 1, y = 2 B. x = 2, y = 1 C. no solution D. infinite number of solutions