Let S be the set of all strings of 0’s and 1’s of length 3. Define a relation R on S as follows:
a. Proof:
R is reflexive because for each string s in S, s has the same two left-most characters as s.
R is symmetric because for all strings s and t in S, if s has the same two left-most characters as t then t has the same two left-most characters as s.
R is transitive because for all strings s, t, and u in S, if s has the same two left-most characters as t and t has the same two left-most characters as u then s has the same two left-most characters as u.
R is an equivalence relation because it is reflexive, symmetric, and transitive.
b. distinct equivalence classes of R: {000, 001}, {010, 011}, {101, 101}, {110, 111}.
You might also like to view...
The figure shows some faces from the "Guess Who?" game. Decide whether the statement is true or false.
?
There are three faces that have glasses.
?
?
A. True B. False
Solve the problem.A stone is thrown into a pond. A circular ripple is spreading over the pond in such a way that the radius is increasing at the rate of 2.6 feet per second. Find a function, r(t), for the radius in terms of t. Find a function, A(r), for the area of the ripple in terms of r.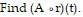 
A. (A ? r)(t) = 2.6?t2 B. (A ? r)(t) = 5.2?t2 C. (A ? r)(t) = 6.76?2t D. (A ? r)(t) = 6.76?t2
Provide an appropriate response.Find the double integral over the rectangular region R with the given boundaries.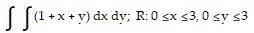
A. 36 B. 18 C. 27 D. 10
Determine the limit by sketching an appropriate graph.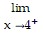
f(x), where f(x) =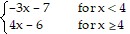 
A. -5 B. -19 C. -6 D. 10