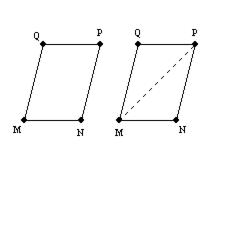
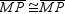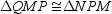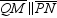Provide the missing statements abd nissing reasons for the proof of this theorem.“If both pairs of opposite sides of a quadrilateral are congruent, the quadrilateral is a parallelogram.”Given: Quad. MNPQ;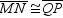
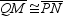
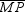
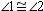
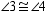
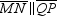
and 
Prove: MNPQ is a parallelogramS1. R1. GivenS2. Draw diagonal 
R2.S3. R3. IdentityS4. R4. SSSS5. 
R5.S6. R6. If 2 lines are cut by a trans. so that alternate interior anglesare congruent, these lines are parallel.S7. 
R7.S8. 
R8.S9. R9.
What will be an ideal response?
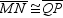and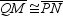 
R2. Through 2 points, there is exactly one line.
S3. 
S4. 
R5. CPCTC
S6. 
R7. CPCTC
R8. Same as reason 6
S9. MNPQ is a parallelogram
R9. Definition of parallelogram
You might also like to view...
Perform the indicated operations. Write the result in the form a + bj.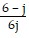
A. - 
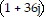
B.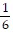 
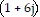
C.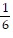 
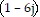
D. -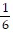 
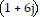
Answer the question about the given function.Given the function f(x) =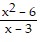 
, is the point (-1, 
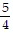) on the graph of f?
A. Yes B. No
Write the statement as an equivalent statement that does not use the if . . . then connective. Remember that p ? q is equivalent to ~p ? q.If you can't find the right dress for the party, then you make one yourself.
A. You can find the right dress for the party and you do not make one yourself. B. You can't find the right dress for the party and you do not make one yourself. C. You can't find the right dress for the party or you do not make one yourself. D. You can find the right dress for the party or you make one yourself.
Tell in which quadrant or on what coordinate axis the point lies.(-14, 17)
A. Quadrant II B. Quadrant IV C. Quadrant III D. Quadrant I