Sketch the indicated set. Describe the boundary of the set. Finally, state whether the set is open, closed or neither.{(x, y) : 1 < (x - 2)2 + y2 ? 3}
A. 
The boundaries are two circles, one of
radius 1 and the other of radius 3, both
centered at (2, 0). The set is neither closed or open.
B. 
The boundary is the circle of radius 3
centered at (2, 0). The interior is the
set of all points within the circle.
The set is open.
C. 
The boundary is the circle of radius 1
centered at (2, 0). The interior is the set
of all points within the circle.
The set is closed.
D. 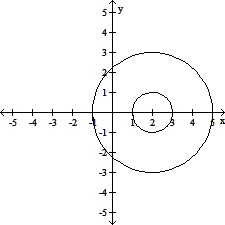
The boundaries are two circles, one of
radius 1 and the other of radius 3, both
centered at (2, 0). The interior is the set
of all points in between the two circles.
The set is closed.
Answer: A
You might also like to view...
The graph of a function f is given. Use the graph to answer the question.How often does the line y = -100 intersect the graph?
A. once B. twice C. three times D. does not intersect
Find the derivative of the function at the given point in the direction of A.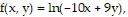
 A = 6i + 8j
A = 6i + 8j
A. - 
B. - 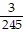
C. 
D. - 
Write the first five terms of the geometric sequence with the given information.The first term is 4 and the common ratio is 3.
A. 12, 36, 108, 324, 972 B. 4, 7, 10, 13, 16 C. 4, 12, 36, 108, 324 D. 3, 12, 48, 192, 768
Decide whether the relation is a function, and give the domain and range.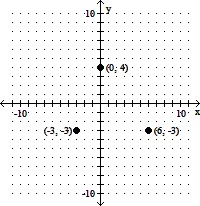
A. Not a function; domain: {-3, 0, 6}; range: {-3, 4} B. Function; domain: {-3, 4}; range: {-3, 0, 6} C. Function; domain: {-3, 0, 6}; range: {-3, 4} D. Not a function; domain: {-3, 4}; range: {-3, 0, 6}