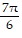Solve the problem.A sailboat leaves port on a bearing of S72°W. After sailing for two hours at 12 knots, the boat turns 90° toward the south. After sailing for three hours at 9 knots on this course, what is the bearing to the ship from port? Round your answer to the nearest 0.1°.
A. S24.6°W
B. S23.6°W
C. N23.6°E
D. N24.6°E
Answer: B
You might also like to view...
Find fx, fy, and fz.f(x, y, z) = cos x sin2 (yz)
A. fx = sin x sin2 (yz); fy = -2z cos x sin (yz) cos (yz); fz = - 2y cos x sin (yz) cos (yz) B. fx = sin x sin2 (yz); fy = - cos x sin (yz) cos (yz); fz = -cos x sin (yz) cos (yz) C. fx = -sin x sin2 (yz); fy = 2z cos x sin (yz) cos (yz); fz = 2y cos x sin (yz) cos (yz) D. fx = -sin x sin2 (yz); fy = z cos x sin (yz) cos (yz); fz = y cos x sin (yz) cos (yz)
The graph of a function f is given. Use the graph to answer the question.Find the values of x, if any, at which f has a relative maximum. What are the relative maxima?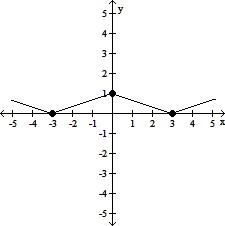
A. f has a relative maximum at x = 0; the relative maximum is 1 B. f has no relative maximum C. f has a relative maximum at x = 3; the relative maximum is 1 D. f has a relative maximum at x = -3 and 3; the relative maximum is 0
Simplify the expression.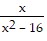 -
- 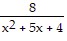
A. 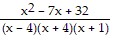
B. 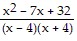
C. 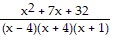
D. 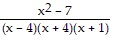
Use trigonometric identities to solve each equation in the interval [0, 2?]3 = 2 cos2 x + 3 sin x
A. 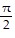 ,
, 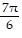 ,
, 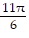
B. 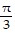 ,
, 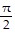 ,
, 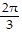
C. 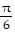 ,
, 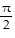 ,
, 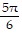
D. 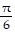 , ?,
, ?,