Solve the problem.Earth has a radius of approximately 6400 kilometers, and Saturn has a radius of approximately 60,300 kilometers (assuming that the planets are spherical). (i) Compute the surface area and volume for both planets. (ii) Which planet has the larger surface-area-to-volume ratio?
A. (i) Surface area of Earth is about 5.15 × 108 square kilometers, volume of Earth is about 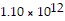 cubic kilometers, surface area of Saturn is about
cubic kilometers, surface area of Saturn is about 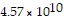 square kilometers, volume of Saturn is about
square kilometers, volume of Saturn is about 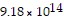 cubic kilometers
cubic kilometers
(ii) Saturn has the larger surface-area-to-volume ratio.
B. (i) Surface area of Earth is about 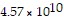 square kilometers, volume of Earth is about
square kilometers, volume of Earth is about 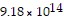 cubic kilometers, surface area of Saturn is about 5.15 × 108 square kilometers, volume of Saturn is about
cubic kilometers, surface area of Saturn is about 5.15 × 108 square kilometers, volume of Saturn is about 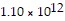 cubic kilometers
cubic kilometers
(ii) Saturn has the larger surface-area-to-volume ratio.
C. (i) Surface area of Earth is about 5.15 × 108 square kilometers, volume of Earth is about 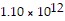 cubic kilometers, surface area of Saturn is about
cubic kilometers, surface area of Saturn is about 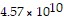 square kilometers, volume of Saturn is about
square kilometers, volume of Saturn is about 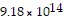 cubic kilometers
cubic kilometers
(ii) Earth has the larger surface-area-to-volume ratio.
D. (i) Surface area of Earth is about 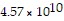 square kilometers, volume of Earth is about
square kilometers, volume of Earth is about 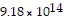 cubic kilometers, surface area of is about 5.15 × 108 square kilometers, volume of Saturn is about
cubic kilometers, surface area of is about 5.15 × 108 square kilometers, volume of Saturn is about 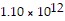 cubic kilometers
cubic kilometers
(ii) Earth has the larger surface-area-to-volume ratio.
Answer: C
You might also like to view...
Find the sum Sn of the first n terms of the geometric sequence. -8, -16, -32, -64, -128, . . . ; n = 9
A. -4108 B. -4051 C. -4088 D. -4086
Solve the problem.Stephanie is at the Mall and wants to stop at the bank on the way home. How many different direct routes can she take to make the trip from the Mall to her house, stopping at the bank on the way?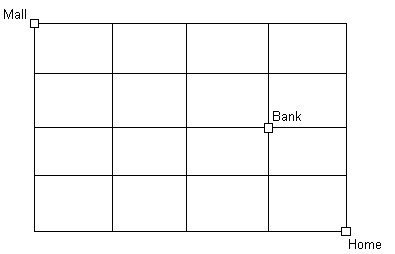
A. 24 B. 40 C. 48 D. 30
Graph the equation.(x - 1)2 + y2 = 36 
A. 
B. 
C. 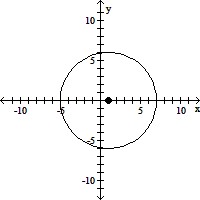
D. 
Solve the system using Gaussian elimination.
?

What will be an ideal response?