Solve the problem.The graph below shows the position s = f(t) of a body moving back and forth on a coordinate line. (a) When is the body moving away from the origin? Toward the origin? At approximately what times is the (b) velocity equal to zero? (c) Acceleration equal to zero? (d) When is the acceleration positive? Negative?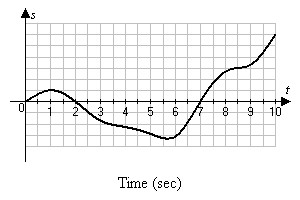
What will be an ideal response?
(a). Moving towards to origin on (1, 2) and (5.7, 7); moving away from the origin on (0, 1), (2, 5.7), and (7, 10).
(b). Velocity is zero at the extrema. These occur at t ? 1 sec and t ? 5.7 sec.
(c). Acceleration is zero at the inflection points. These occur at t ?2.3 sec, t ? 4 sec, t ? 5.1 sec, t ? 7 sec, and t ? 8.5 sec.
(d). Acceleration is positive where f(t) is concave up and negative where it is concave down. Acceleration is positive on (2.3, 4), (5.1, 7), and (8.5, 10). Acceleration is negative on (0, 2.3), (4, 5.1), and (7, 8.5).
You might also like to view...
Solve the problem.In a school survey, students showed these preferences for instructional materials. Answer the question. 
About how many students would you expect to prefer radio in a school of 300 students?
A. About 108 students B. About 15 students C. About 5 students D. About 54 students
Write a formula for the general term (the nth term) of the arithmetic sequence. Then use the formula for an to find a20, the 20th term of the sequence.an = an-1 - 10, a1 = 36
A. an = 26n + 36, a20 = 556 B. an = -10n + 46, a20 = -154 C. an = 36n + 46, a20 = 766 D. an = -10n + 26, a20 = -174
Find the quotient and simplify.
÷ 
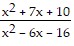
A. -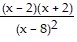 
B. 
C. - 
D. -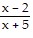 
Solve the problem.Approximate the area under the graph of f(x) = 2x2 + x + 3 from -2 to 1 by partitioning the interval into 3 subintervals of equal length and choosing t to be the left endpoint.
A. 26 B. 13 C. 16 D. 22