Complete the following: (i) Find the x- and y-intercepts. (ii) Determine the multiplicity of each zero of f. (iii) Graph y = f(x).f(x) = x2(x + 7)(x - 7)
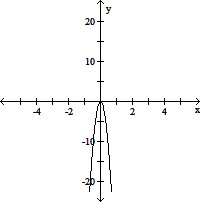
A. (i) x-ints are -7, 0, and 7; the y-int is 0
(ii) 0 has multiplicity 2;
-7 and 7 each have multiplicity 1
(iii)
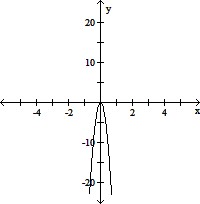
B. (i) x-ints are 0, and -7; the y-int is 0
(ii) 0 and -7 each have multiplicity 2;
(iii)
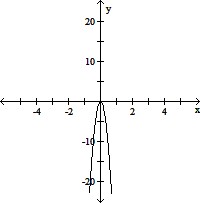
C. (i) x-ints are 0, and 7; the y-int is 0
(ii) 0 and 7 each have multiplicity 2;
(iii)

D. (i) x-ints are -7 and 7; the y-int is -49
(ii) -7 and 7 each have multiplicity 1
(iii)
Answer: A
You might also like to view...
Provide an appropriate response. A function is considered to be an even function if f(-x) = f(x). That is, the function is even if the value of a function for a given number is the same as the value of the function for the opposite of the given number. A function is considered to be an odd function if f(-x) = f(x). That is, the function is odd if the value of the function for a given number is the opposite of the value of the function for the opposite of the given number. For example, if for a certain function f(2) = 5 and f(-2) = 5, then it is even; and if for a certain function f(7) = -2 and f(-7) = 2, then it is odd.Given the function f(x) = x2 + 1, is the function even, odd, or neither? Evaluate f(3), f(-3), f(1), and f(-1) to make this determination.
A. odd B. even C. neither
Solve.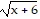 +
+ 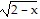 = 4
= 4
A. -2
B. 0
C. 2, -2
D. 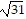 , -2
, -2
Solve. = x + 3
= x + 3
A. 0
B. 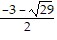
C. 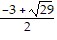
D. 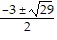
Simplify by combining like terms.7z - z
A. 6z B. 7z - 1 C. 6z2 D. -7z2