Use the Principle of Mathematical Induction to show that the statement is true for all natural numbers n.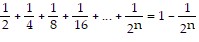
What will be an ideal response?
When 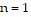 , the left side of the statement is
, the left side of the statement is 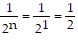 , and the right side of the
, and the right side of the
statement is 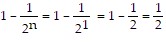 , so the statement is true when
, so the statement is true when 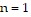 .
.
Assume the statement is true for some natural number k. Then,
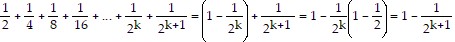 .
.
So the statement is true for 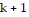 . Conditions I and II are satisfied; by the Principle of Mathematical Induction, the statement is true for all natural numbers.
. Conditions I and II are satisfied; by the Principle of Mathematical Induction, the statement is true for all natural numbers.
You might also like to view...
Choose the expression that is equivalent to the given rational number.
A. 
B. 0.64
C. 0.6
D. 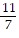
Solve the problem.Find the number of terms in the following arithmetic progression 1, 3, 5, 7, . . . , 31
A. 16 B. 18 C. 31 D. 15
Answer the question appropriately.Find the area of the "triangular" region in the first quadrant that is bounded above by the curve 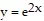 , below by the curve y = ex, and on the right by the line x = ln 4.
, below by the curve y = ex, and on the right by the line x = ln 4.
A. 4
B. 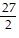
C. 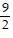
D. 4 ln 4
Evaluate.Let a = 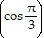 i +
i +  j , b =
j , b = 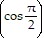 i +
i +  j. Find a + b.
j. Find a + b.
A.  i -
i -  j
j
B.  i +
i + 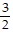 j
j
C.  i +
i + 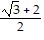 j
j
D. 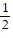 i +
i +  j
j