Solve the problem.The unit vectors u and v are combined to produce two new vectors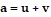 
and 
Show that a and b are orthogonal. Assume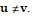 
What will be an ideal response?
u = ux i + uyj and v = vx i + vyj , so
a = u + v = (ux + vx) i + (uy + vy)j and b = u - v = (ux - vx) i + (uy - vy)j
Take the dot product a ? b:
a ? b = (u + v) ? (u - v) = (ux + vx)(ux - vx) + (uy + vy)(uy - vy)
= 
- 
+ 
- 
= (
+ 
) - (
+ 
)
= 
- 
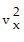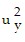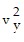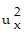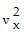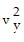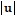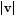= 1 - 1 = 0
Since the dot product of the two non-zero vectors is zero they are orthogonal.
You might also like to view...
Express the quantified statement in an equivalent way, that is, in a way that has exactly the same meaning.Some orchids are not flowers.
A. Some flowers are not orchids. B. All orchids are not flowers. C. All orchids are flowers. D. Not all orchids are flowers.
Provide an appropriate response.(56 + 89) + 103 = 24856 + (89 + 103) = 248This is an example of the 
.
A. commutative property of addition B. associative property of addition C. associative property of multiplication D. commutative property of multiplication
The graph of the given function is drawn with a solid line. The graph of a function, g(x), transformed from this one is drawn with a dashed line. Find a formula for g(x).f(x) = x2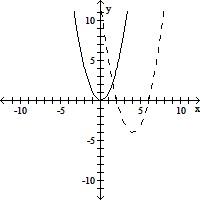
A. g(x) = (x - 2)2 - 4 B. g(x) = 2(x + 4)2 C. g(x) = -2(x - 4)2 D. g(x) = (x - 4)2 - 4
Give the equation of the oblique asymptote, if any, of the function. f(x) =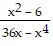 
A. y = 0 B. no oblique asymptote C. y = x - 6 D. y = 36x