Find a matrix A and a column matrix B that describe the following tables involving credits and tuition costs. Find the matrix product AB, and interpret the significance of the entries of this product.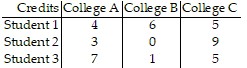
?
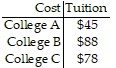
A.
AB = 
Tuition for Student 1 is $1091, tuition for Student 2 is $839, and tuition for Student 3 is $779.
B.
AB = 
Tuition for Student 1 is $1097, tuition for Student 2 is $839, and tuition for Student 3 is $803.
C.
AB = 
Tuition for Student 1 is $1098, tuition for Student 2 is $837, and tuition for Student 3 is $793.
D.
AB =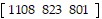 
Tuition for Student 1 is $1108, tuition for Student 2 is $823, and tuition for Student 3 is $801.
Answer: C
You might also like to view...
Solve the problem.A rectangular swimming pool has a parabolic drain plate at the bottom of the pool. The drain plate is shaped like the region between y =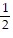 
x2 and the line y = 
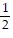from x = -1 to x = 1. The pool is 10 ft by 20 ft and 8 ft deep. If the drain plate is designed to withstand a fluid force of 200 lb, how high can the pool be filled without exceeding this limitation?
A. 5 ft 1 in. B. 4 ft 11 in. C. 5 ft 6 in. D. 5 ft 9 in.
Solve the problem.
Determine the coupon rate of a bond issued by Bank.
A. 4.950% B. 4.800% C. 5.050% D. 4.650%
Write the exponential equation in its equivalent logarithmic form.10-3 = 0.001
A. log3-3 = 0.10
B. log10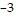
= 0.001
C. log30.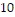
= -3
D. log10
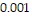= -3
Examine the function given below for relative extrema and saddle points.
?
?
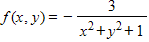
A. The function has a relative minimum at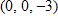 
.
B. The function has a relative maximum at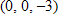 
.
C. The function has a saddle point at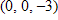 
.
D. The function has a relative maximum at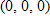 
.
E. The function has a relative minimum at 
.