A mouse is placed at random in one of five compartments of a maze. The probability of it going to another compartment is given in the following transition matrix. Using this information, solve the problem.1 2345
Find the probability that a mouse ends up in compartment 5, if it started in compartment 1.
A. 0.519
B. 0.491
C. 0.481
D. 0.509
Answer: D
You might also like to view...
Provide an appropriate response.Use a calculator to graph the function f to see whether it appears to have a continuous extension to the origin. If it does, use Trace and Zoom to find a good candidate for the extended function's value at x = 0. If the function does not appear to have a continuous extension, can it be extended to be continuous at the origin from the right or from the left? If so, what do you think the extended function's value(s) should be? f(x) =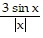 
A. continuous extension exists at origin; f(0) = 0 B. continuous extension exists at origin; f(0) = 3 C. continuous extension exists from the right; f(0) = 3 continuous extension exists from the left; f(0) = -3 D. continuous extension exists from the right; f(0) = 1 continuous extension exists from the left; f(0) = -1
Solve the problem.The distance, in feet, that a car travels down the side of a mountain in each consecutive second is modeled by a sequence whose general term is an = 46n - 18, where n is the number of seconds. Find the distance the car travels in the fifth second.
A. 166 ft B. 212 ft C. 230 ft D. 248 ft
The equation is in the form y = mx + b. Identify m and b.y = x - 6
A. m = 1; b = -6 B. m = 0; b = 6 C. m = -6; b = -1 D. m = -6; b = 1
Evaluate the function.For f(x) = x2 + 9x, find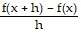 
.
A. 2xh + h + 9h B. 2x + h + 9 C. 2x + h - 9 D. x