Use the principle of mathematical induction to show that the mathematical statement is true for all natural numbers n.Sn: 6 + 12 + 18 + . . . + 6n = 3n(n + 1)
What will be an ideal response?
| S1: | 6 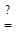 (3 ? 1)(1 + 1) (3 ? 1)(1 + 1) |
 3 ? 2
3 ? 26 = 6 ?
Sk: 6 + 12 + 18 + . . . + 6k = 3k(k + 1)
Sk+1: 6 + 12 + 18 + . . . + 6(k + 1) = 3(k + 1)(k + 2)
We work with Sk. Because we assume that Sk is true, we add the next multiple of 6, namely
6(k+1), to both sides.
6 + 12 + 18 + . . . + 6k + 6(k + 1) = 3k(k + 1) + 6(k + 1)
6 + 12 + 18 + . . . + 6(k + 1) = (k + 1)(3k + 6)
6 + 12 + 18 + . . . + 6(k + 1) = 3(k + 1)(k + 2)
We have shown that if we assume that Sk is true, and we add 6(k+1) to both sides of Sk, then Sk+1 is also true. By the principle of mathematical induction, the statement Sn is true for every positive integer n.
You might also like to view...
Find the probability. Round to the nearest ten-thousandth when necessary.A family has five children. The probability of having a girl is 1/2. What is the probability of having exactly 2 girls and 3 boys?
A. 0.6252 B. 0.0312 C. 0.3125 D. 0.0625
Find the composition. If f(x) = 6x + 4 and g(x) = x + 5, find (g ? f)(x)
A. 6x + 9 B. 6x2 + 34x + 20 C. 6x2 + 34 D. 6x + 34
Find the vertex, focus, and directrix of the parabola.- 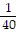 x2 = y
x2 = y
A. Vertex: V(0, 0); focus: F(0, -10); directrix: y = 10 B. Vertex: V(0, 0); focus: F(-20, 0); directrix: x = 10 C. Vertex: V(0, 0); focus: F(0, 10); directrix: y = -10 D. Vertex: V(0, 0); focus: F(0, -10); directrix: y = -10
Find the distance between P and Q.P(6, 2), Q(-7, -3)
A. 65
B. 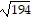
C. 8
D. 12