Use the Principle of Mathematical Induction to show that the statement is true for all natural numbers n.
What will be an ideal response?
When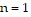 
, the left side of the statement is 
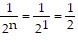, and the right side of the
statement is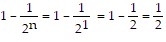 
, so the statement is true when 
.
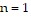Assume the statement is true for some natural number k. Then,
.
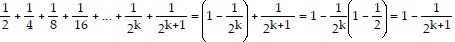So the statement is true for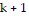 
. Conditions I and II are satisfied; by the Principle of Mathematical Induction, the statement is true for all natural numbers.
You might also like to view...
Provide an appropriate response.A surveyor sights to a point across a pond, then makes a right angle, measures 50-ft and sights the same point across the pond with a 34° angle. Find the distance across the pond where the surveyor began.
A. 41.45 ft B. 33.73 ft C. 27.96 ft D. 74.13 ft
Use a calculator to find a decimal approximation for the indicated function value. Round your answer to four decimal places.csc 2.65
A. 2.1185 B. -0.8816 C. -1.1343 D. 0.4720
Graph the equation using the indicated viewing window.y = x2 + 2;X min = -5X max = 5X scl = 1Y min = -20Y max = 20Y scl = 5
A.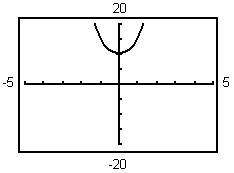 
B. 
C. 
D. 
Solve the equation. 4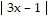
- 8 = -6Round to the nearest hundredth if necessary.
A. 0.17, 0.5 B. 2.5 C. 0.5 D. -1.83, 2.5