Divide.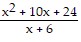
A. x3 - 18
B. x2 + 4
C. x - 18
D. x + 4
Answer: D
You might also like to view...
Use Taylor series to evaluate the limit.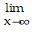
x3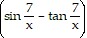
A. - 
B. - 
C. - 
D. - 
Solve the problem.A rocket is 34 feet from a satellite when it begins accelerating away from the satellite at a constant rate of 20 feet per second per second. The distance, in feet, between the rocket and the satellite is modeled by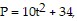 
where t is the number of seconds since the rocket started accelerating. Use the model to find and interpret the result when t = 9.
A. When t = 9, P = 844; After 9 seconds, the distance between the rocket and the satellite is 844 feet. B. When t = 115, P = 9; After 115 seconds, the distance between the rocket and the satellite is 9 feet. C. When t = 124, P = 9; After 124 seconds, the distance between the rocket and the satellite is 9 feet. D. When t = 9, P = 810; After 9 seconds, the distance between the rocket and the satellite is 810 feet.
Determine either absolute convergence, conditional convergence or divergence for the series.
A. Converges conditionally B. Converges absolutely C. Diverges
Without graphing, find the vertex.f(x) = -(x - 3)2 - 3
A. (0, -3) B. (3, -3) C. (-3, 0) D. (3, 3)