Provide an appropriate response.The Cobb-Douglas production function for a company is given by P(k, l) = 70k3/4l1/4 where P is the monthly production value when k is the number of units of capital and l is the number of units of labor. Suppose that capital costs $450 per unit, labor costs $75 per unit, and the total cost of capital and labor is limited to $60,000. Use Lagrange multipliers to write the system of equations you would use to find the number of units of capital and labor that maximize production.
What will be an ideal response?
(You do not have to solve this system!)
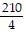 k-1/4l1/4 - 450? = 0 k-1/4l1/4 - 450? = 0 |
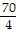 k3/4l-3/4 - 75? = 0 k3/4l-3/4 - 75? = 0 |
| 450k + 75l - 60,000 = 0 |
Mathematics
You might also like to view...
Solve the problem.Find the dimensions of a box with largest volume if it lies in the first octant, three of its faces lie in the coordinate planes, and the box lies beneath (or touching) the plane with equation 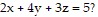
A. 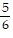 by
by 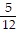 by
by 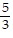
B. 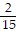 by
by 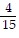 by
by 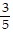
C.  by
by 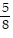 by
by 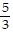
D. 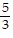 by
by 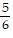 by
by 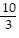
Mathematics
Perform the indicated operation

Mathematics
Plot the two points given by the ordered pairs.A(0, -4), B(-3, 2)
A. 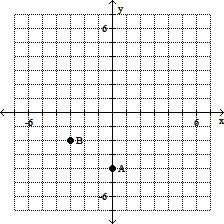
B. 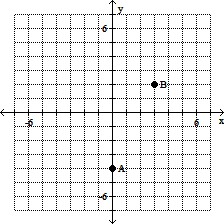
C. 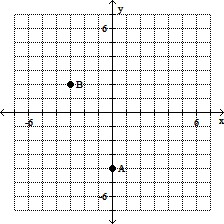
D. 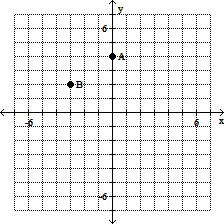
Mathematics
Find the determinant of 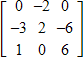
A. -14 B. 24 C. -4 D. -24 E. -34
Mathematics