The displacement d (in meters) of an object at time t (in seconds) is given. Describe the motion of the object. What is the maximum displacement from its resting position, the time required for one oscillation, and the frequency?d = 4 cos (5t)
A. simple harmonic; 4 m;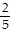 
? sec; 
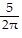oscillations/sec
B. simple harmonic; 4 m;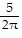 
sec; 
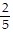? oscillations/sec
C. simple harmonic; 4 m; 5 ? sec;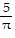 
oscillations/sec
D. simple harmonic; -4 m;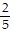 
? sec; 
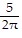oscillations/sec
Answer: A
You might also like to view...
Find the x-intercepts for the parabola whose equation is given. If the x-intercepts are irrational, round your answers to the nearest tenth.y = x2 + 4x - 7
A. x-intercepts: none B. x-intercept: (4, 0) C. x-intercepts: (-2 ± 3.3, 0) D. x-intercepts: (-4, 0) and (3, 0)
Solve the problem.If a tone is formed from the combination of two component frequencies, F1 and F2 , as is done with touch-tone phones, then the tone can be represented as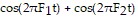 
if the intensities of the components are equal. For the two component frequencies 
and 
rewrite this expression as a product of trigonometric functions and graph the result in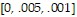 
-4.0px;" /> by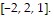 
A. 2 cos(995?t) cos(995?t)
[0, .005, .001] by [-2, 2, 1]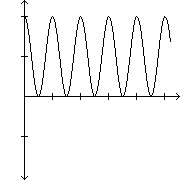
B. 2 cos(995?t) cos(265?t)
[0, .005, .001] by [-2, 2, 1]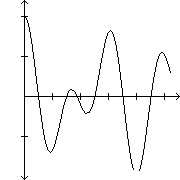
C. 2 cos(1990?t) cos(1990?t)
[0, .005, .001] by [-2, 2, 1]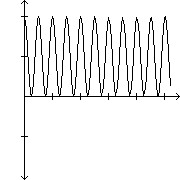
D. 2 cos(1990?t) cos(530?t)
[0, .005, .001] by [-2, 2, 1]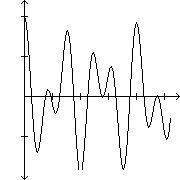
Solve the problem.Lisa stashed in an envelope on her dresser $454 each week for 9 weeks. Estimate the total amount she saved by rounding the weekly amount to the nearest hundred. Also find the exact amount she saved.
A. Estimate: $4,500; exact: $4,050 B. Estimate: $4,050; exact: $4,086 C. Estimate: $4,050; exact: $4,050 D. Estimate: $4,500; exact: $4,086
Factor the trinomial completely. If the trinomial cannot be factored, say it is prime.m2 + mn - 56n2
A. (m + 8n)(m - 7n) B. (m + 8n)(m + 7n) C. (m - 8n)(m + 7n) D. (m - 8n)(m - 7n)