Find the center, transverse axis, vertices, foci, and the equations of the asymptotes of the hyperbola.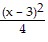 - 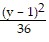= 1

A. center: (3, 1)
transverse axis: y = 1
vertices: (1, 1) and (5, 1)
foci: (3 - 2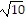, 1) and (3 + 2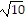, 1)
asymptotes: y - 1 = - 3(x - 3) and y - 1 = 3(x - 3)
B. center: (3, 1)
transverse axis: x = 3
vertices: (3, -1) and (3, 3)
foci: (3, 1 - 2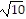) and (3, 1 + 2)
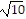asymptotes: y + 1 = - 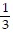(x + 3) and y + 1 = 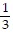(x + 3)
C. center: (1, 3)
transverse axis: y = 1
vertices: (-1, 3) and (3, 3)
foci: (1 - 2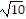, 3) and (1 + 2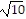, 3)
asymptotes: y - 3 = - 3(x - 1) and y - 3 = 3(x - 1)
D. center: (3, 1)
transverse axis: x = 3
vertices: (-3, 1) and (9, 1)
foci: (3 - 2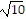, 1) and (3 + 2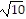, 1)
asymptotes: y - 1 = - 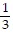(x - 3) and y - 1 = 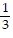(x - 3)