Are the following two statements logically equivalent? Justify your answer.
(a) A real number is less than 1 only if its reciprocal is greater than 1.
(b) Having a reciprocal greater than 1 is a sufficient condition for a real number to be less than 1.
These two statements are not logically equivalent.
Explanation 1: The first statement is equivalent to “If a real number is less than 1, then its reciprocal
is greater than 1” and the second statement is equivalent to “If the reciprocal of a real number is
greater than 1, then the number is less than 1.” Thus the second statement is the converse of the first,
and a conditional statement and its converse are not logically equivalent.
Explanation 2: The first statment is false. For example, ?2 is less than 1, but its reciprocal, ?1
2 is greater than 1. However, the second statement is true; if the reciprocal of a real number is greater than 1, then the number itself is positive and is between 0 and 1, and it is impossible for one of a pair of equivalent statements to be true while the other member of the pair is false.
You might also like to view...
Evaluate the function.f(x) = 6x2 + 2x + 5, find f(-5)
A. 140 B. 157 C. 145 D. -35
In the problem, sin ? and cos ? are given. Find the exact value of the indicated trigonometric function.sin ? = 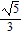 , cos ? =
, cos ? = 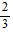 Find tan ?.
Find tan ?.
A. 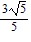
B. 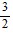
C. 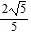
D. 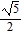
Solve the problem.If the lengths of the sides of a square are tripled, by what factor will the area change?
A. 6 B. 27 C. 3 D. 9
Identify the radicand.
A. y + 2
B. 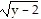
C. 
D. y - 2