Solve the differential equation.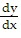
= 6x
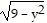
A. y = sin (3x2 + C)
B. y = 3 sin (3x2 + C)
C. y = 3 sin-1 (3x2 + C)
D. y = sin-1 (3x2 + C)
Answer: B
You might also like to view...
A recursion formula and the initial term(s) of a sequence are given. Write out the first five terms of the sequence.a1 = 1, an+1 = 6an
A. 1, 6, 36, 216, 1296 B. 6, 36, 216, 1296, 7776 C. 6, 7, 8, 9, 10 D. 1, 7, 13, 19, 25
Decide whether or not the points are the vertices of a right triangle.Consider the three points A = (-3, 3), B = (-1, 7), C = (1, 6). Determine whether the triangle ABC is a right triangle. Explain your reasoning.
A. The side lengths of triangle ABC are d(A, B) = 3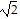
, d(A, C) = 5, d(B, C) = 
.
[d(A, B)]2 + [d(B, C)]2 = (3
)2 + (
)2 = 18 + 5 = 23
[d(A, C)]2 = 52 = 25
Since [d(A, C)]2 ? [d(A, B)]2 + [d(B, C)]2, triangle ABC is not a right triangle.
B. The side lengths of triangle ABC are d(A, B) = 2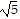
, d(A, C) = 2
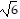, d(B, C) = 2.
[d(A, B)]2 + [d(B, C)]2 = (2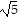
)2 + 22 = 20 + 4 = 24
[d(A, C)]2 = (2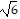
)2 = 24
Since [d(A, C)]2 = [d(A, B)]2 + [d(B, C)]2, triangle ABC is a right triangle.
C. The side lengths of triangle ABC are d(A, B) = 2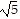
, d(A, C) = 5, d(B, C) = 2.
[d(A, B)]2 + [d(B, C)]2 = (2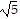
)2 + 22 = 20 + 4 = 24
[d(A, C)]2 = 52 = 25
Since [d(A, C)]2 ? [d(A, B)]2 + [d(B, C)]2, triangle ABC is not a right triangle.
D. The side lengths of triangle ABC are d(A, B) = 2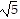
, d(A, C) = 5, d(B, C) = 
.
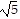[d(A, B)]2 + [d(B, C)]2 = (2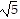
)2 + (
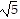)2 = 20 + 5 = 25
[d(A, C)]2 = 52 = 25
Since [d(A, C)]2 = [d(A, B)]2 + [d(B, C)]2, triangle ABC is a right triangle.
If the following defines a one-to-one function, find its inverse. If not, write "Not one-to-one."{(5, -15), (14, -15), (12, -11)}
A. {(5, -15), (-15, 14), (-11, 12)} B. Not one-to-one C. {(-15, 5), (-15, 14), (-11, 12)} D. {(-15, 5), (12, 14), (-11, -15)}
Use the circle graph to solve the problem.A survey of the 7872 vehicles on the campus of State University yielded the following circle graph.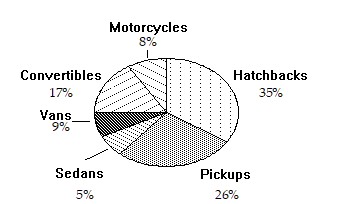 
Find the number of hatchbacks. Round your result to the nearest whole number.
A. 2362 B. 35 C. 2755 D. 5117